Script Modelos lineales

Descargar script

Descargar script en pdf

NOTA: Para descargar los datos, dar click en el boton. Aparece una pantalla con los datos, luego dar click derecho y poner guardar como (save as). Guardar el txt donde van a trabajar

Descargar datos

R.1

Llamo los datos, los coloco en un dataframe y convierto las columnas en variables

reg.data<-read.table("tannin.txt",header=T)
attach(reg.data)
names(reg.data)

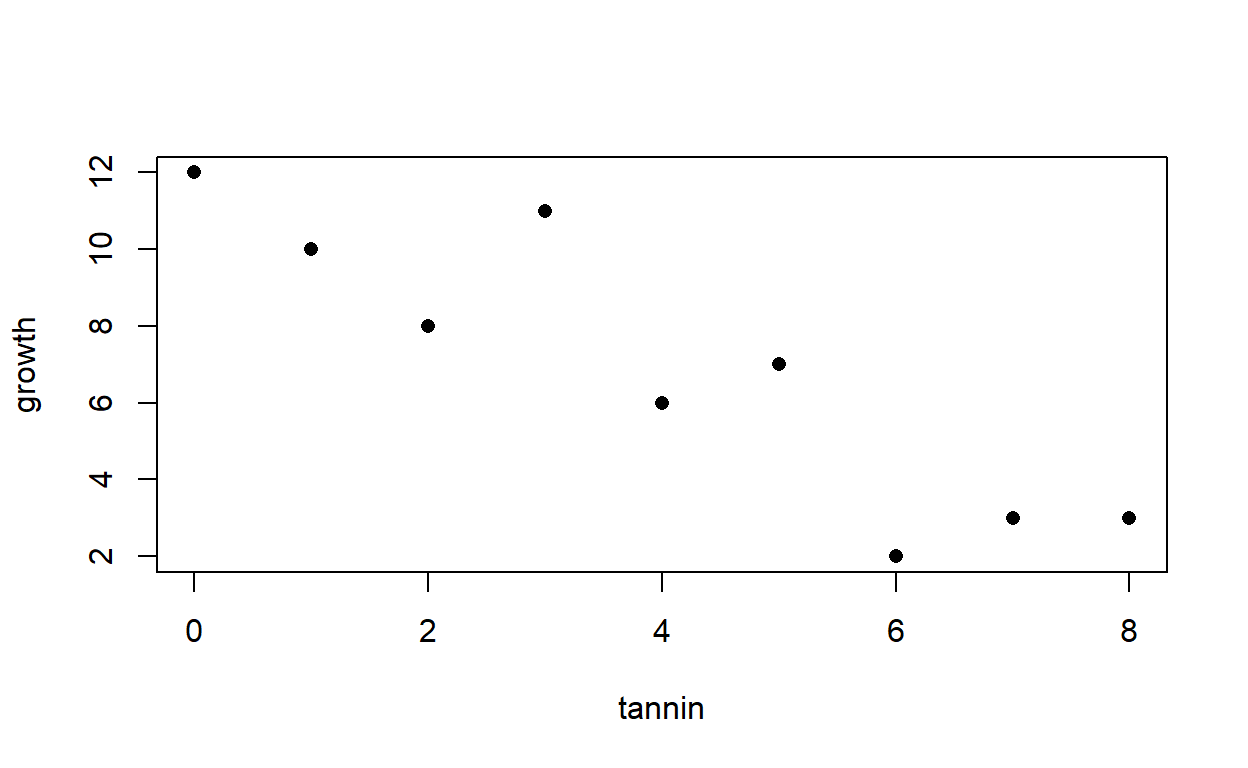
Gráfico

par(mfrow=c(1,1))
plot(tannin,growth,pch=16)

¿La tendencia de la variable de respuesta es a incrementar o a disminuir con la explicatoria? tendencia a disminuir

¿Es factible que los datos sean explicados por una línea horizontal? H0.

plot(tannin,growth,pch=16)
abline(mean(growth),0)

La H0 no parece factible, entonces b es probablemente dif de 0 y negativa

¿Si existe una tendencia es recta o curva? relación recta, entonces proponemos el modelo \(y=a+bx+e\)

¿La dispersión de los datos es uniforme a lo largo de la línea o cambia sistemáticamente con la variable explicatoria?. Dispersión muy uniforme, la ordenada al origen es dif de 0 entonces a es prob mayor que 0.

¿A ojo cuales son los valores de a y b? Como podemos hacer este proceso sistemático y preciso?

C.1

R.2

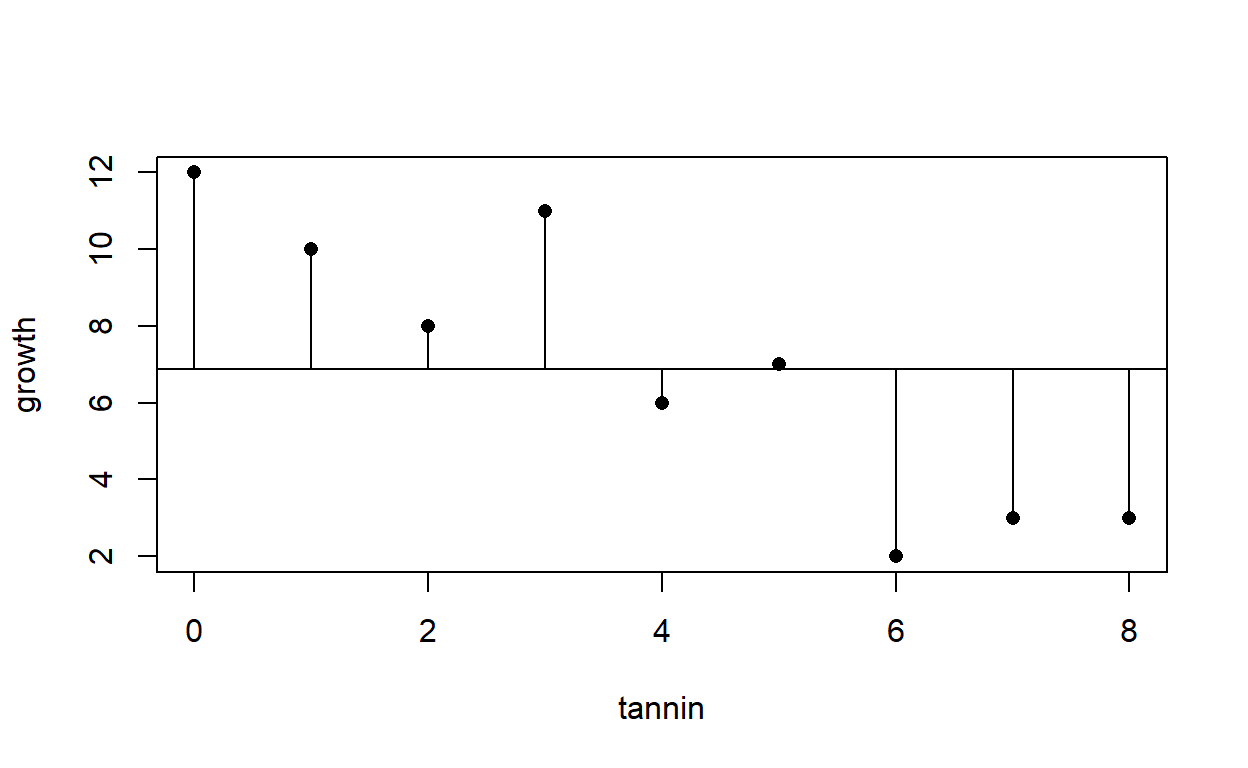
Y la variación total de y es la dispersión de los datos alrededor de y barra.

La Suma de Cuadrados Total es \(SCT= \sum(y-\overline{y})^2\)

plot(tannin,growth,pch=16)
abline(mean(growth),0)
for (i in 1:9) lines(c(tannin[i],tannin[i]),c(growth[i],mean(growth)))

La mejor recta ajustada por el método de mínimos cuadrados es aquella que minimiza la Suma de Cuadrados de las desviaciones de los valores de y de la línea ajustada \(\hat{y}\), \(SCE=\sum(y - \hat{y})^2\)

plot(tannin,growth,pch=16) 
abline(lm(growth~tannin))

ysomb <- predict(lm(growth ~ tannin))
plot(tannin,growth,pch=16) 
abline(lm(growth~tannin))
for(i in 1:9) lines(c(tannin[i], tannin[i]), c(growth[i], ysomb[i]))

C.2

R.3

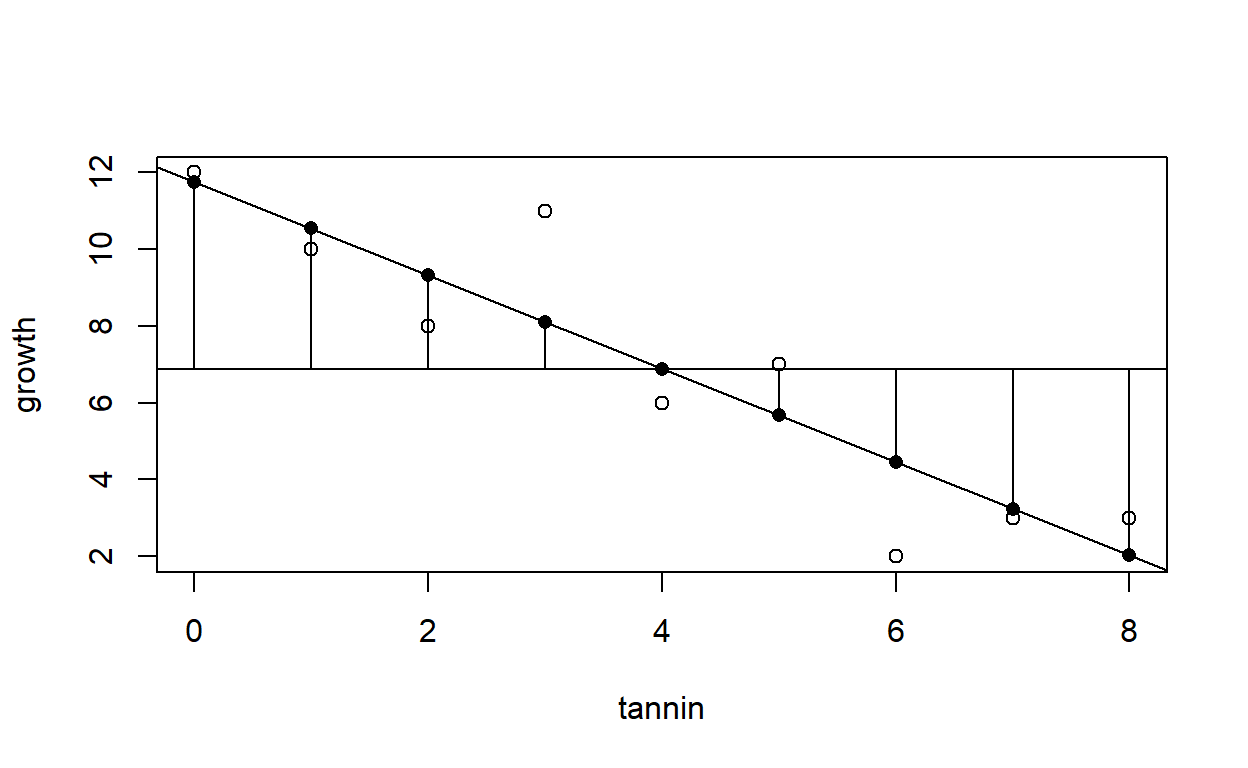
Ahora bien, una tercera cantidad es la Suma de Cuadrados de la Regresión (es decir del efecto de la variable predictora)

\[SCR = SCTotal - SCError\]

plot(tannin, growth, type = "n") 
abline(mean(growth), 0) 
modelito <- lm(growth ~ tannin) 
abline(modelito) 
for(i in 1:9) lines(c(tannin[i], tannin[i]), c(mean(growth), predict(modelito)[i])) 
points(tannin,predict(modelito), pch = 16) 
points(tannin, growth)

C.3

R.4

Empezamos a ajustar los modelos: modelo nulo - solo la media

Nulo <- lm(growth ~ 1) 
names(Nulo)

 [1] "coefficients"  "residuals"     "effects"       "rank"         
 [5] "fitted.values" "assign"        "qr"            "df.residual"  
 [9] "call"          "terms"         "model"        

anova(Nulo) 

Analysis of Variance Table

Response: growth
          Df Sum Sq Mean Sq F value Pr(>F)
Residuals  8 108.89  13.611               

Nulo$df.residual 

[1] 8

Nulo$coefficients 

(Intercept) 
   6.888889 

Nulo$fitted.values

       1        2        3        4        5        6        7 
6.888889 6.888889 6.888889 6.888889 6.888889 6.888889 6.888889 
       8        9 
6.888889 6.888889 

plot(tannin, growth) 
abline(a=Nulo$coe, b=0) 
abline(Nulo$coe, 0)

Es decir solo se ha ajustado la media que no ofrece información importante

Agregamos el efecto del tannin

Tanino <- update(Nulo, . ~ . + tannin)
Tanino

Call:
lm(formula = growth ~ tannin)

Coefficients:
(Intercept)       tannin  
     11.756       -1.217  

anova(Tanino)

Analysis of Variance Table

Response: growth
          Df Sum Sq Mean Sq F value    Pr(>F)    
tannin     1 88.817  88.817  30.974 0.0008461 ***
Residuals  7 20.072   2.867                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Tanino$coefficients

(Intercept)      tannin 
  11.755556   -1.216667 

summary(Tanino)

Call:
lm(formula = growth ~ tannin)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.4556 -0.8889 -0.2389  0.9778  2.8944 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  11.7556     1.0408  11.295 9.54e-06 ***
tannin       -1.2167     0.2186  -5.565 0.000846 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.693 on 7 degrees of freedom
Multiple R-squared:  0.8157,    Adjusted R-squared:  0.7893 
F-statistic: 30.97 on 1 and 7 DF,  p-value: 0.0008461

O bien pedimos la secuencia de ajustes, que produce estos cambios en devianza

anova(Nulo, Tanino)

Analysis of Variance Table

Model 1: growth ~ 1
Model 2: growth ~ tannin
  Res.Df     RSS Df Sum of Sq      F    Pr(>F)    
1      8 108.889                                  
2      7  20.072  1    88.817 30.974 0.0008461 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

summary(Tanino)

Call:
lm(formula = growth ~ tannin)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.4556 -0.8889 -0.2389  0.9778  2.8944 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  11.7556     1.0408  11.295 9.54e-06 ***
tannin       -1.2167     0.2186  -5.565 0.000846 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.693 on 7 degrees of freedom
Multiple R-squared:  0.8157,    Adjusted R-squared:  0.7893 
F-statistic: 30.97 on 1 and 7 DF,  p-value: 0.0008461

Si queremos, podemos guardar los valores ajustados y los residuales en la base de datos:

reg.data$ajustados <- fitted.values(Tanino) 
reg.data$residuales <- residuals(Tanino)
reg.data

  growth tannin ajustados residuales
1     12      0 11.755556  0.2444444
2     10      1 10.538889 -0.5388889
3      8      2  9.322222 -1.3222222
4     11      3  8.105556  2.8944444
5      6      4  6.888889 -0.8888889
6      7      5  5.672222  1.3277778
7      2      6  4.455556 -2.4555556
8      3      7  3.238889 -0.2388889
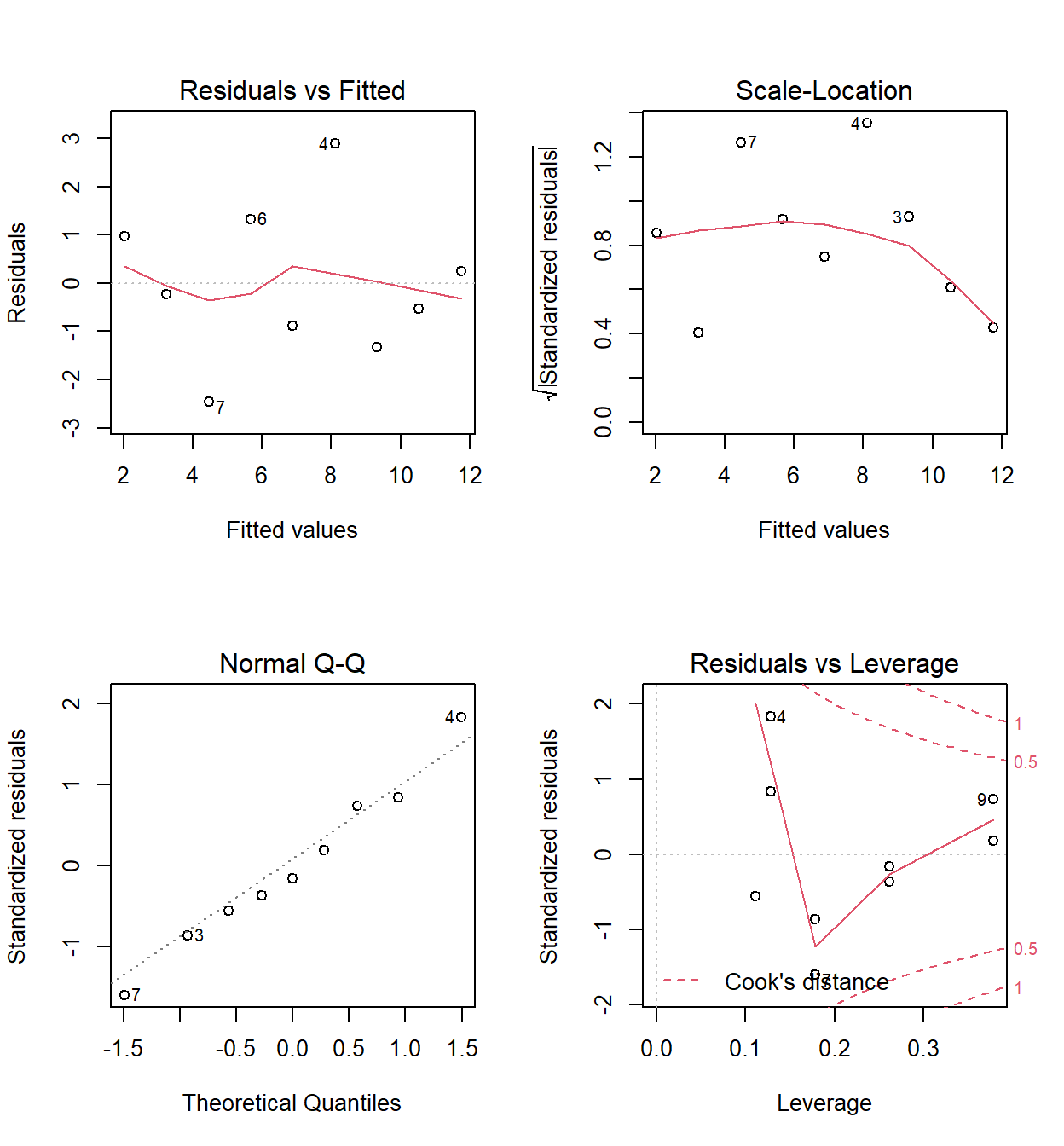
9      3      8  2.022222  0.9777778

Para inspeccionar qué tan bueno es el modelo existen algunos recursos gráficos donde se examinan la distribución de los residuales y los puntos extremos que que pueden “cargar” el valor numérico de los parámetros:

par(mfcol=c(2,2))
plot(Tanino)

Extra

Una función muy interesante para evaluar un modelo es check_model del paquete performance(Lüdecke et al. 2021). Recuerda que puedes instalarlo así:

# Debido a que performance requiere del paquete see para graficar, es bueno instalar ambos
install.packages(c("performance", "see"))

Cargamos las librerias

library(performance)
library(see)

Ahora usamos la función

check_model(Tanino)

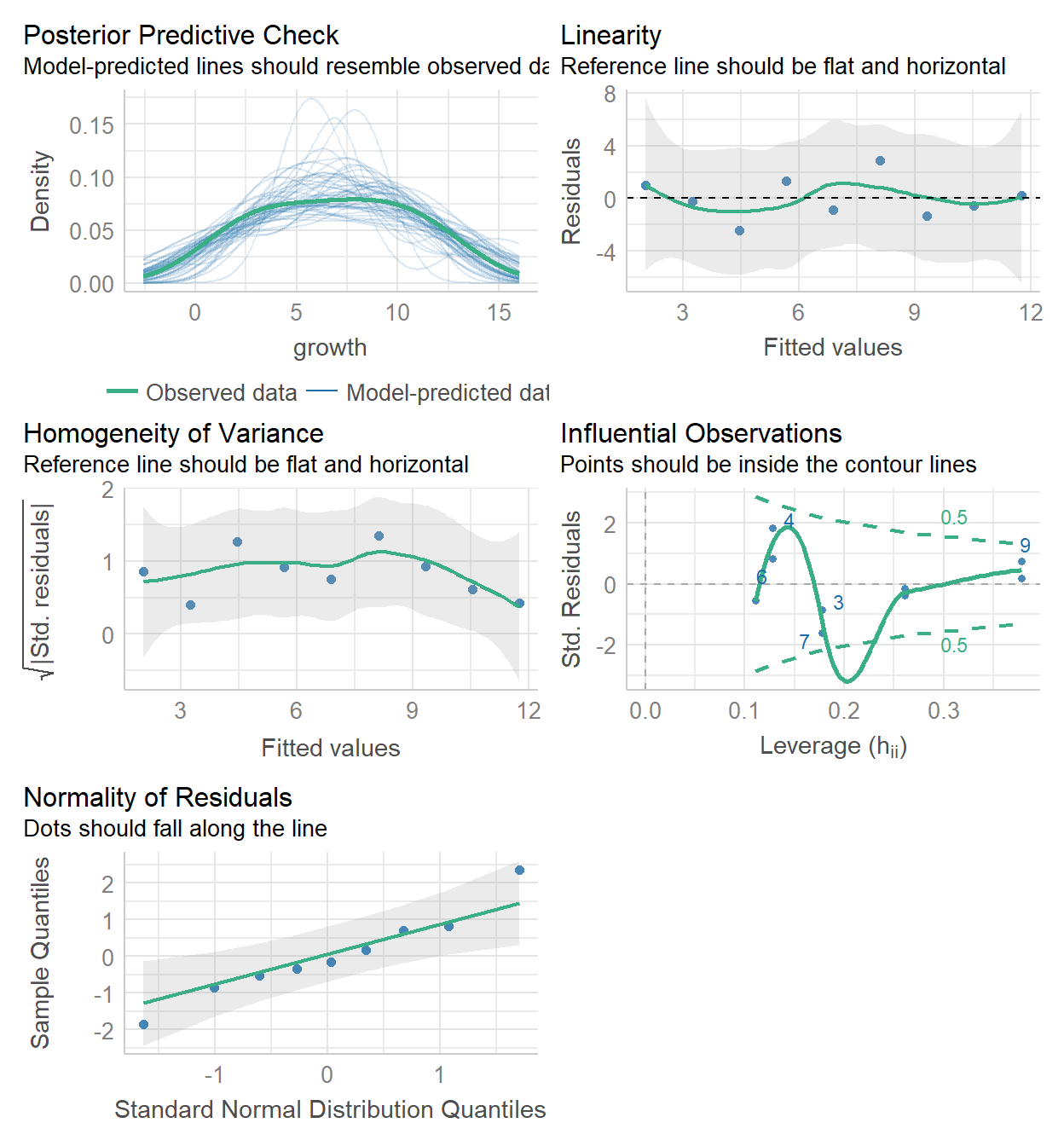
Si son fans de el diagnóstico numérico:

# Por defecto usa los residuales estandarizados
check_normality(Tanino)

OK: residuals appear as normally distributed (p = 0.990).

shapiro.test(rstandard(Tanino)) 

    Shapiro-Wilk normality test

data:  rstandard(Tanino)
W = 0.98664, p-value = 0.9896

check_heteroskedasticity(Tanino) # Breusch-Pagan test (1979).

OK: Error variance appears to be homoscedastic (p = 0.843).

check_outliers(Tanino)

OK: No outliers detected.
- Based on the following method and threshold: cook (0.77).
- For variable: (Whole model)

Examinamos un modelo sin el dato extremo:

Sindat7 <- lm(growth[-7] ~ tannin[-7]) 
summary(Sindat7)

Call:
lm(formula = growth[-7] ~ tannin[-7])

Residuals:
    Min      1Q  Median      3Q     Max 
-1.4549 -0.9572 -0.1622  0.4572  2.6622 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  11.6892     0.8963  13.042 1.25e-05 ***
tannin[-7]   -1.1171     0.1956  -5.712  0.00125 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.457 on 6 degrees of freedom
Multiple R-squared:  0.8446,    Adjusted R-squared:  0.8188 
F-statistic: 32.62 on 1 and 6 DF,  p-value: 0.001247

No ganamos gran cosa

Extra

Podemos obtener los resultados del modelo lineal en formato de dataframe con el paquete broom(Robinson, Hayes, and Couch 2022) y la función tidy

install.packages("broom")

library(broom)
coeftable <- tidy(Sindat7)
coeftable

# A tibble: 2 x 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)    11.7      0.896     13.0  0.0000125
2 tannin[-7]     -1.12     0.196     -5.71 0.00125  

De esta forma podemos reportarla de manera más ordenada en un documento Rmarkdown, Quarto o simplemente guardarla como un csv para luego copiarla a mano en un documento word

Así se puede guardar

write.csv(coeftable, # objeto a guardar
          file = "modelo2.csv") # nombre del archivo

Para predecir valores usamos:

predict(Tanino, list(tannin =7.5))

       1 
2.630556 

par(mfrow=c(1,1)) 
ls() 

[1] "coeftable" "i"         "modelito"  "Nulo"      "reg.data" 
[6] "Sindat7"   "Tanino"    "ysomb"    

rm(list=ls(all=TRUE))

Fin