Script Análisis exploratorios

NOTA: Para descargar los datos, dar click en el boton. Aparece una pantalla con los datos, luego dar click derecho y poner guardar como (save as). Guardar el csv donde van a trabajar

R.1

ESTE EJEMPLO ES DE DATOS DE EVERITT 04 P. 17. CONSISTE EN INFORMACIÓN SOBRE CONTAMINACIÓN AMBIENTAL EN EU EN ZONAS METROPOLITANAS.

Llamo los datos (ojo que Everitt los tiene en formato dat, si están como txt, hay que llamarlos con read.table)

airpoll<-source("chap2airpoll.dat")$value
ap <- data.frame(airpoll)
# write.csv(ap, "apdf.csv")
adf <- read.csv("airpoll.csv", header = T, sep = ";") #tabla con dato faltante

attach(airpoll)
airpoll

         Rainfall Education Popden Nonwhite NOX SO2 Mortality
akronOH        36      11.4   3243      8.8  15  59     921.9
albanyNY       35      11.0   4281      3.5  10  39     997.9
allenPA        44       9.8   4260      0.8   6  33     962.4
atlantGA       47      11.1   3125     27.1   8  24     982.3
baltimMD       43       9.6   6441     24.4  38 206    1071.0
birmhmAL       53      10.2   3325     38.5  32  72    1030.0
bostonMA       43      12.1   4679      3.5  32  62     934.7
bridgeCT       45      10.6   2140      5.3   4   4     899.5
bufaloNY       36      10.5   6582      8.1  12  37    1002.0
cantonOH       36      10.7   4213      6.7   7  20     912.3
chatagTN       52       9.6   2302     22.2   8  27    1018.0
chicagIL       33      10.9   6122     16.3  63 278    1025.0
cinnciOH       40      10.2   4101     13.0  26 146     970.5
clevelOH       35      11.1   3042     14.7  21  64     986.0
colombOH       37      11.9   4259     13.1   9  15     958.8
dallasTX       35      11.8   1441     14.8   1   1     860.1
daytonOH       36      11.4   4029     12.4   4  16     936.2
denverCO       15      12.2   4824      4.7   8  28     871.8
detrotMI       31      10.8   4834     15.8  35 124     959.2
flintMI        30      10.8   3694     13.1   4  11     941.2
ftwortTX       31      11.4   1844     11.5   1   1     891.7
grndraMI       31      10.9   3226      5.1   3  10     871.3
grnborNC       42      10.4   2269     22.7   3   5     971.1
hartfdCT       43      11.5   2909      7.2   3  10     887.5
houstnTX       46      11.4   2647     21.0   5   1     952.5
indianIN       39      11.4   4412     15.6   7  33     968.7
kansasMO       35      12.0   3262     12.6   4   4     919.7
lancasPA       43       9.5   3214      2.9   7  32     844.1
losangCA       11      12.1   4700      7.8 319 130     861.8
louisvKY       30       9.9   4474     13.1  37 193     989.3
memphsTN       50      10.4   3497     36.7  18  34    1006.0
miamiFL        60      11.5   4657     13.5   1   1     861.4
milwauWI       30      11.1   2934      5.8  23 125     929.2
minnplMN       25      12.1   2095      2.0  11  26     857.6
nashvlTN       45      10.1   2082     21.0  14  78     961.0
newhvnCT       46      11.3   3327      8.8   3   8     923.2
neworlLA       54       9.7   3172     31.4  17   1    1113.0
newyrkNY       42      10.7   7462     11.3  26 108     994.6
philadPA       42      10.5   6092     17.5  32 161    1015.0
pittsbPA       36      10.6   3437      8.1  59 263     991.3
portldOR       37      12.0   3387      3.6  21  44     894.0
provdcRI       42      10.1   3508      2.2   4  18     938.5
readngPA       41       9.6   4843      2.7  11  89     946.2
richmdVA       44      11.0   3768     28.6   9  48    1026.0
rochtrNY       32      11.1   4355      5.0   4  18     874.3
stlousMO       34       9.7   5160     17.2  15  68     953.6
sandigCA       10      12.1   3033      5.9  66  20     839.7
sanfrnCA       18      12.2   4253     13.7 171  86     911.7
sanjosCA       13      12.2   2702      3.0  32   3     790.7
seatleWA       35      12.2   3626      5.7   7  20     899.3
springMA       45      11.1   1883      3.4   4  20     904.2
syracuNY       38      11.4   4923      3.8   5  25     950.7
toledoOH       31      10.7   3249      9.5   7  25     972.5
uticaNY        40      10.3   1671      2.5   2  11     912.2
washDC         41      12.3   5308     25.9  28 102     968.8
wichtaKS       28      12.1   3665      7.5   2   1     823.8
wilmtnDE       45      11.3   3152     12.1  11  42    1004.0
worctrMA       45      11.1   3678      1.0   3   8     895.7
yorkPA         42       9.0   9699      4.8   8  49     911.8
youngsOH       38      10.7   3451     11.7  13  39     954.4
names(airpoll)

[1] "Rainfall"  "Education" "Popden"    "Nonwhite"  "NOX"      
[6] "SO2"       "Mortality"

Exploración Univariada

Comenzamos por ver el vector de medias y varianzas

#mean(airpoll) #sd(airpoll)^2

summary(airpoll)

    Rainfall       Education         Popden        Nonwhite    
 Min.   :10.00   Min.   : 9.00   Min.   :1441   Min.   : 0.80  
 1st Qu.:32.75   1st Qu.:10.40   1st Qu.:3104   1st Qu.: 4.95  
 Median :38.00   Median :11.05   Median :3567   Median :10.40  
 Mean   :37.37   Mean   :10.97   Mean   :3866   Mean   :11.87  
 3rd Qu.:43.25   3rd Qu.:11.50   3rd Qu.:4520   3rd Qu.:15.65  
 Max.   :60.00   Max.   :12.30   Max.   :9699   Max.   :38.50  
      NOX              SO2           Mortality     
 Min.   :  1.00   Min.   :  1.00   Min.   : 790.7  
 1st Qu.:  4.00   1st Qu.: 11.00   1st Qu.: 898.4  
 Median :  9.00   Median : 30.00   Median : 943.7  
 Mean   : 22.65   Mean   : 53.77   Mean   : 940.4  
 3rd Qu.: 23.75   3rd Qu.: 69.00   3rd Qu.: 983.2  
 Max.   :319.00   Max.   :278.00   Max.   :1113.0  
summary(airpoll$SO2)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   1.00   11.00   30.00   53.77   69.00  278.00

vease la diferencia entre la media y la mediana para reconocer desviaciones, calculese el intervalo intercuartiles (3er-1er).

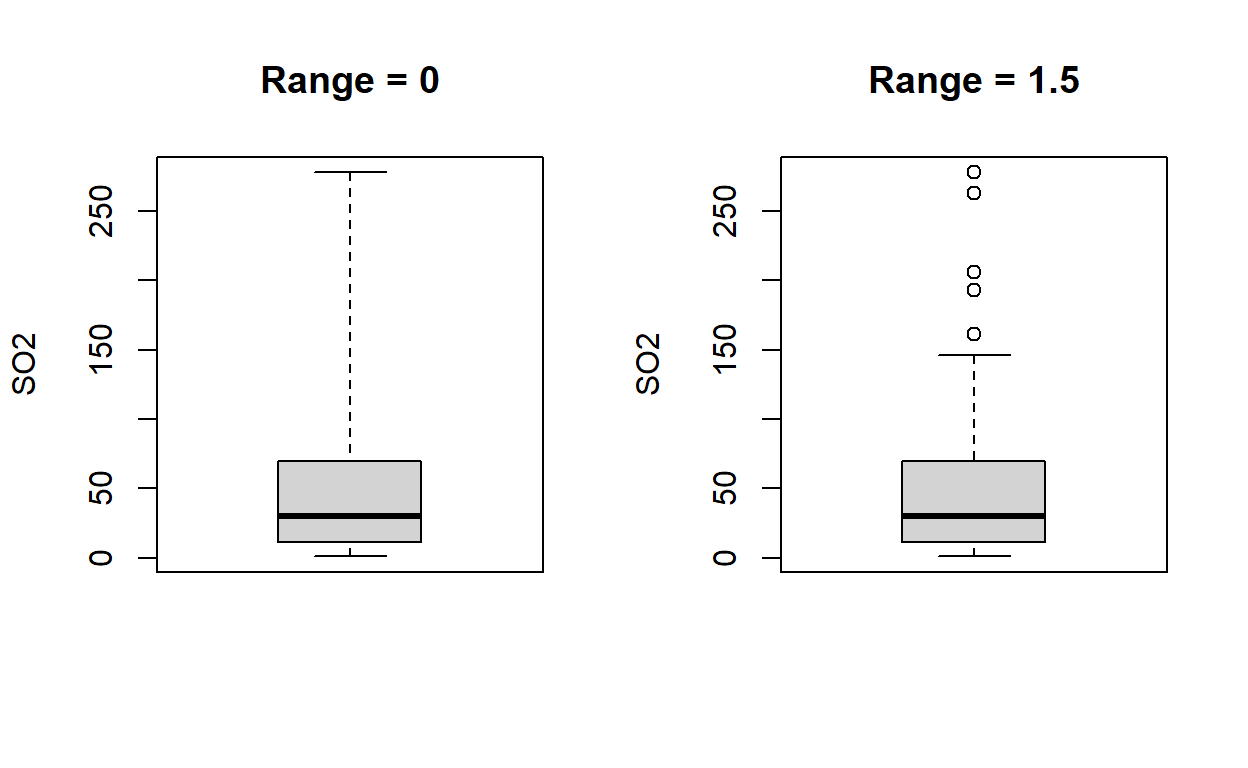
Boxplot

#windows()
boxplot(SO2, range=0, ylab="SO2", main= "Range 0") # en este caso, los "bigotes" del boxplot ubican el máximo (1) y el mínimo (278).

boxplot(SO2, ylab="SO2", main= "Range 1.5") #en este caso, la función se ejecuta con range = 1.5 por defecto.


iqSO2<-69-11
iqSO2

[1] 58

Una buena regla de dedo para identificar datos atípicos es: que los puntos que caen mas allá del 3er+1.5(intercuartil) o mas bajo que 1er-1.5(intercuartil) son valores atípicos.

atipicossup<-69+(iqSO2*1.5)
  atipicossup

[1] 156
atipicosinf<-abs(11-(iqSO2*1.5))
  atipicosinf

[1] 76
hist(SO2,lwd=2)
abline(v = 156, col = "blue")

¿Cuales son los valores atípicos para SO2? Ahora veamos lo que considera R como atípicos por default

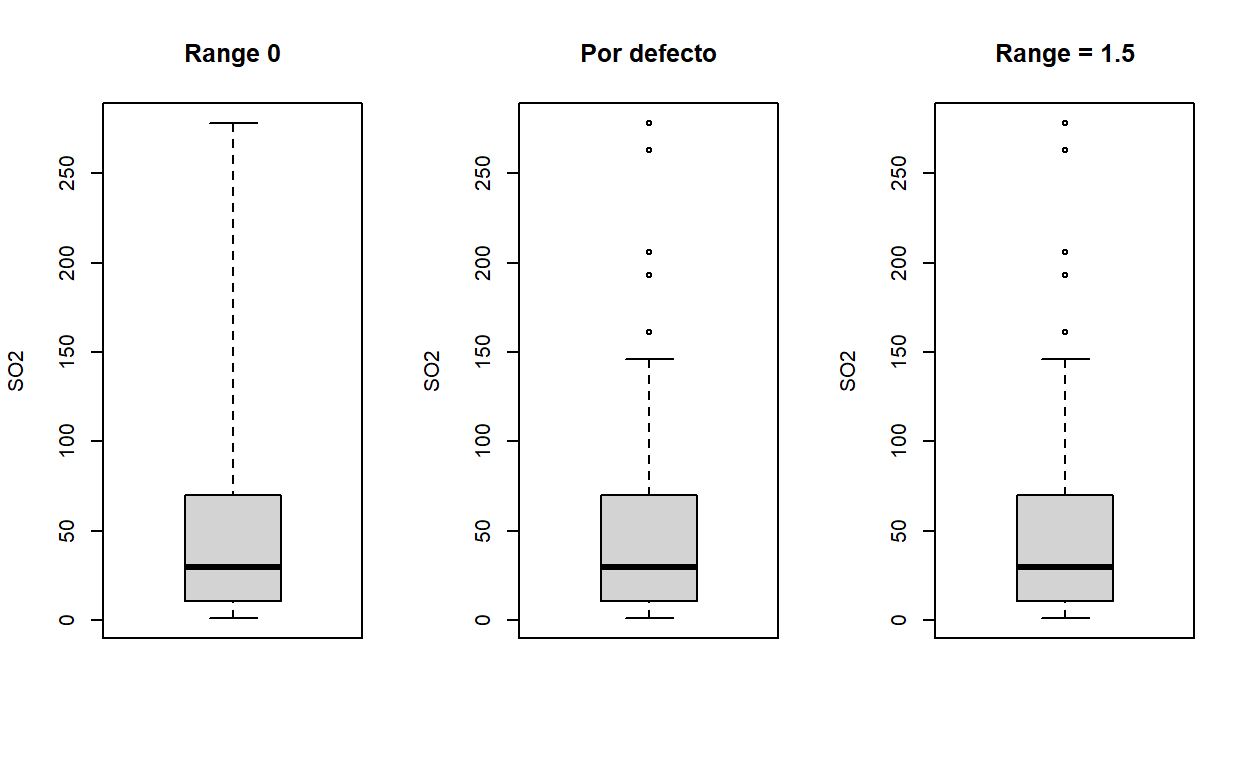
par(mfrow=c(1,3))
boxplot(SO2, range=0, ylab="SO2", main= "Range 0")
boxplot(SO2, ylab="SO2", main="Por defecto")
boxplot(SO2, range=1.5, ylab="SO2", main= "Range = 1.5")

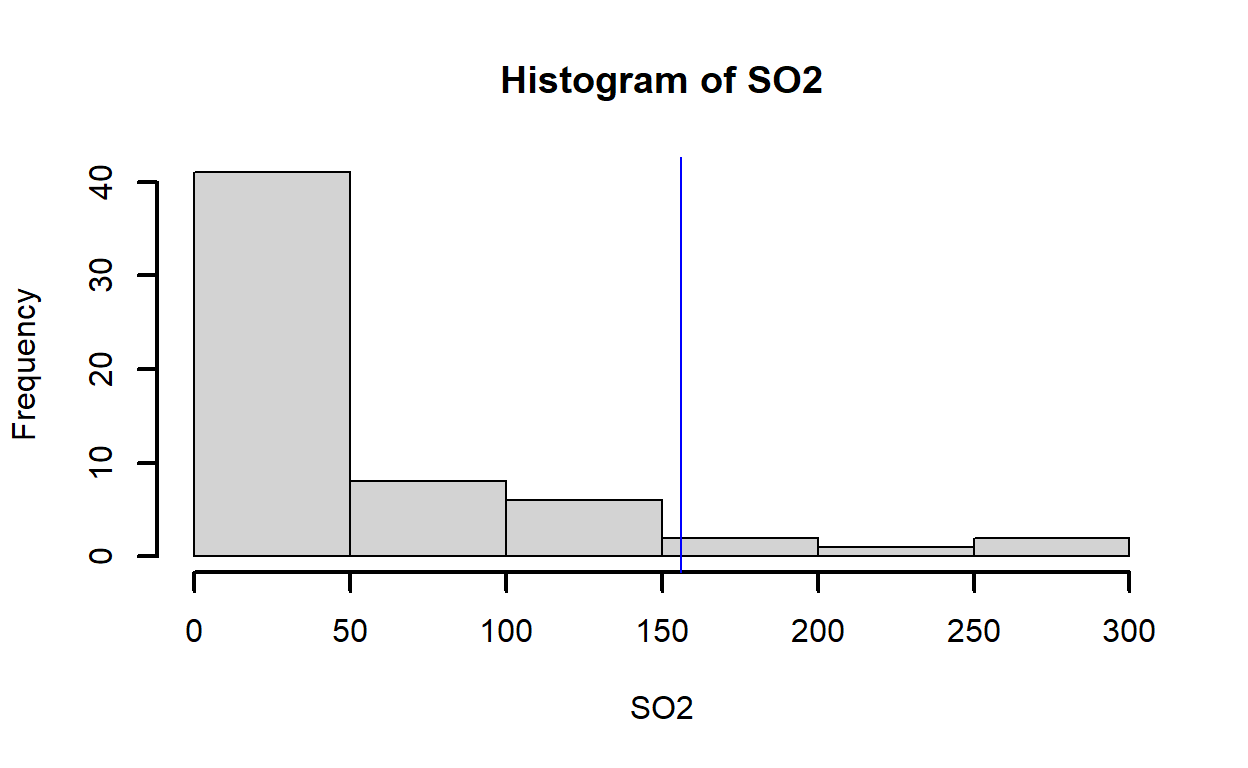
Histogramas

Veamos las distribuciones de todas

par(mfrow=c(3,3))
hist(SO2,lwd=2); abline(v = c(53.77, 30), col = c("blue", "red"))
hist(Rainfall,lwd=2)
hist(Education,lwd=2)
hist(Popden,lwd=2)
hist(Nonwhite,lwd=2)
hist(NOX,lwd=2)
hist(Mortality,lwd=2)

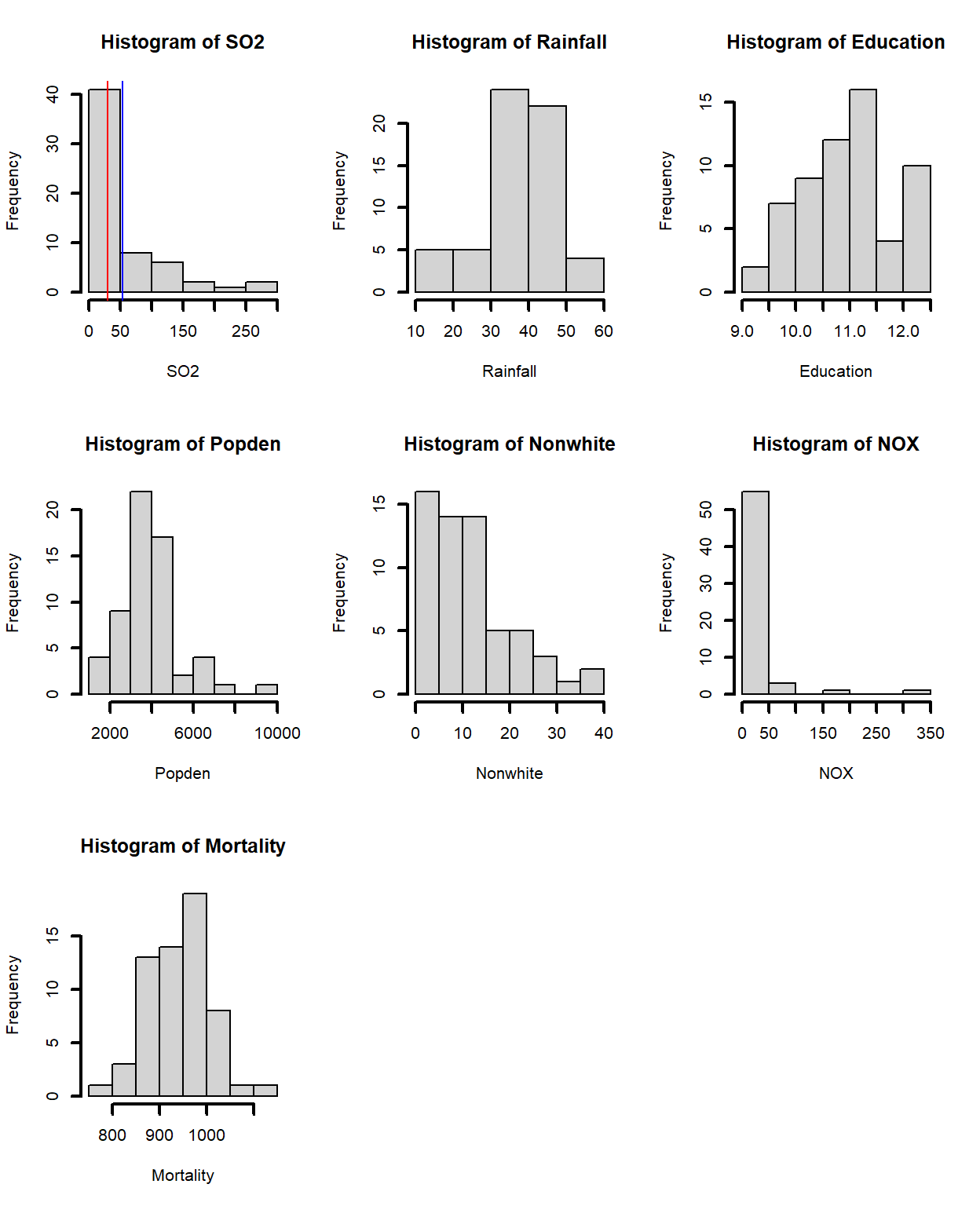
¿reconocen desviaciones negativas o positivas? Son normales?

Kurtosis y simetría

En este caso se necesita el paquete datawizard (Patil et al. 2022) para correr las pruebas de kurtosis y simetria

Para instalarlo pueden usar

install.packages("datawizard")

¿Cómo se ve sin sesgo y curtosis?

Simetría (Skewness)

library(datawizard)

norm <- rnorm(1000) #Genero 1000 datos con distribución normal

sk <- skewness(norm)
sk

Skewness |    SE
----------------
   0.080 | 0.077
ku <- kurtosis(norm)
ku

Kurtosis |    SE
----------------
  -0.089 | 0.154
hist(norm, freq = F)
lines(density(norm))
text(x= -2, y=0.3, label= paste("Skewness =", round(sk$Skewness,2))) 
text(x= 2, y=0.3, label= paste("Kurtosis =",  round(ku$Kurtosis,2)))

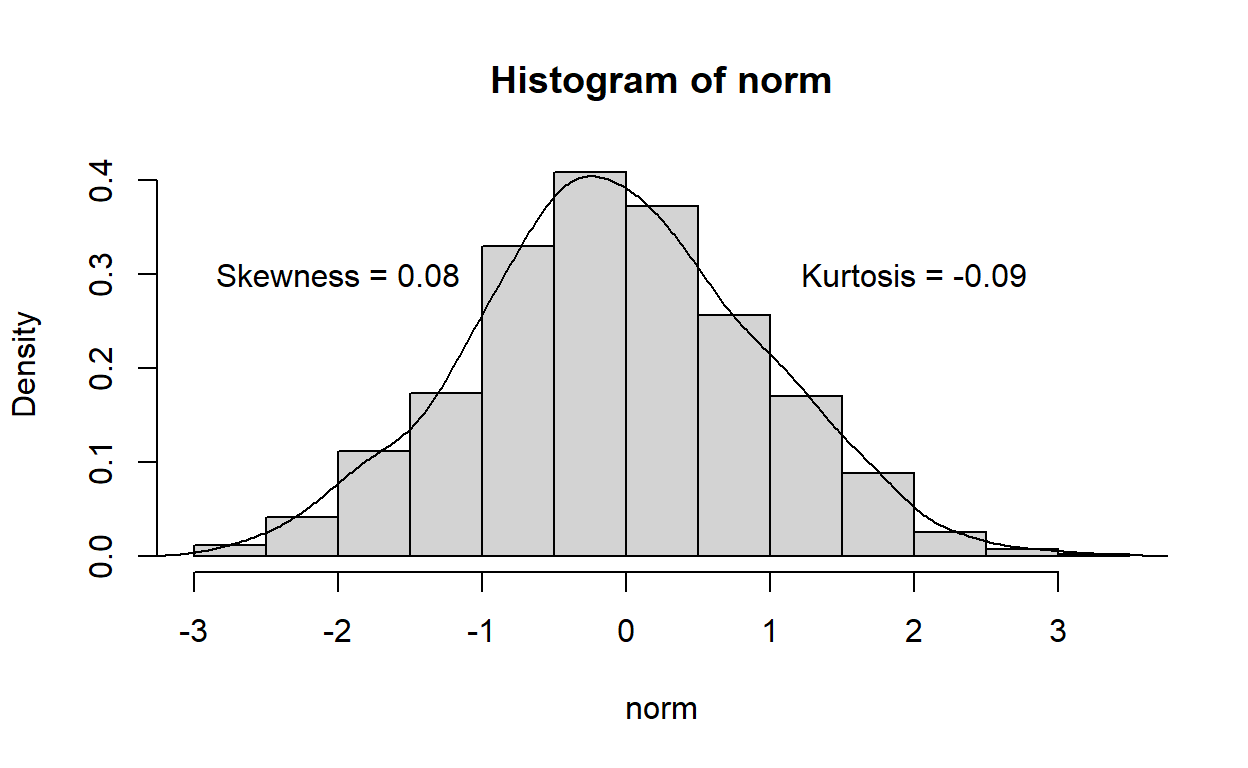
Ahora con nuestros datos

skewness(SO2)

Skewness |    SE
----------------
   1.912 | 0.301
kurtosis(SO2)

Kurtosis |    SE
----------------
   3.552 | 0.559
hist(SO2,freq = F)
lines(density(SO2))
text(x= 100, y=0.01, label= "Skewness = 1.912")
text(x= 250, y=0.01, label= "Kurtosis = 3.552")


skewness(log(SO2+1))

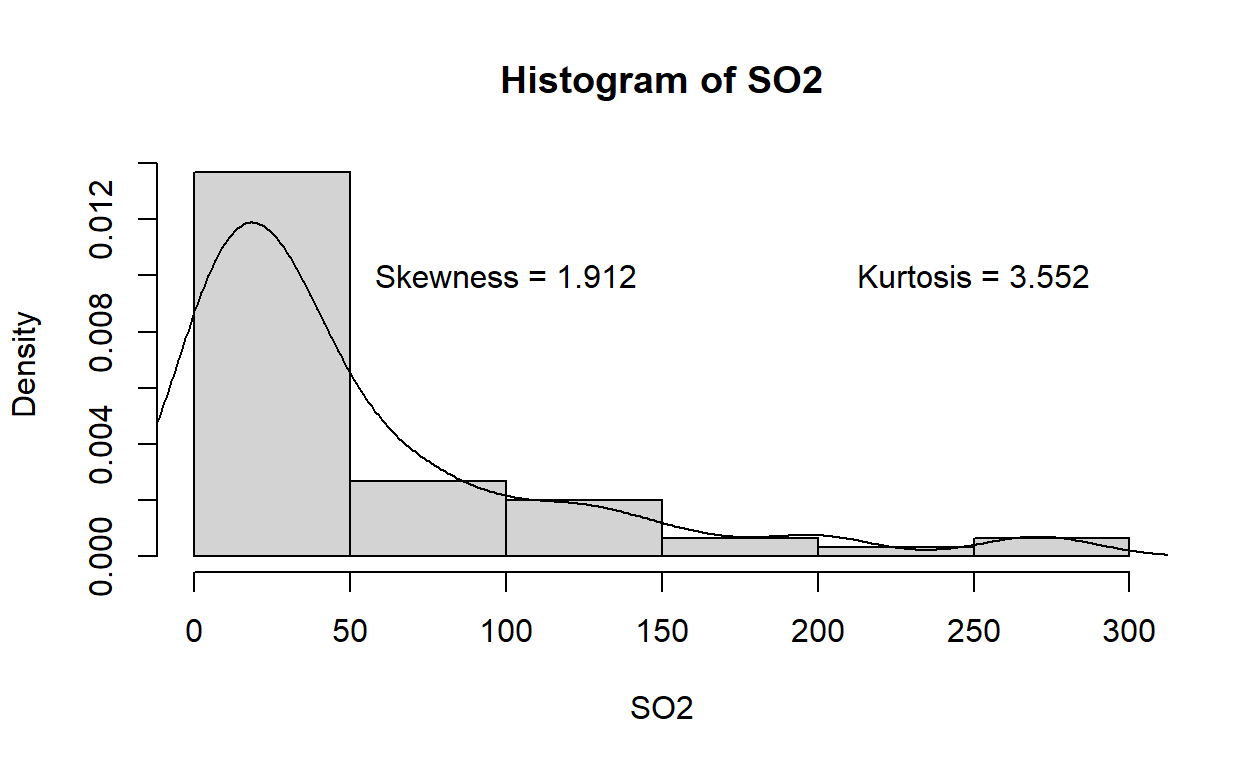
Skewness |    SE
----------------
  -0.443 | 0.301
kurtosis(log(SO2+1))

Kurtosis |    SE
----------------
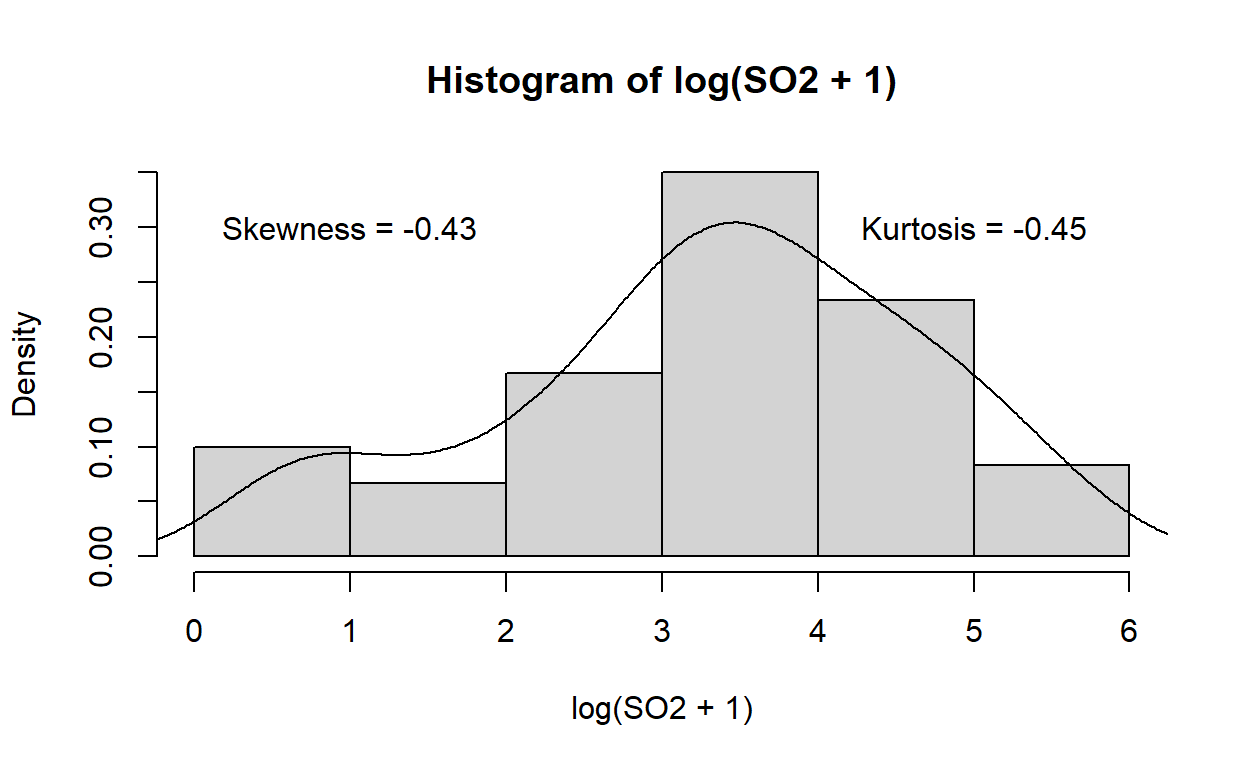
  -0.390 | 0.559
hist(log(SO2+1),freq = F)
lines(density(log(SO2+1)))
text(x= 1, y=0.3, label= "Skewness = -0.43")
text(x= 5, y=0.3, label= "Kurtosis = -0.45")


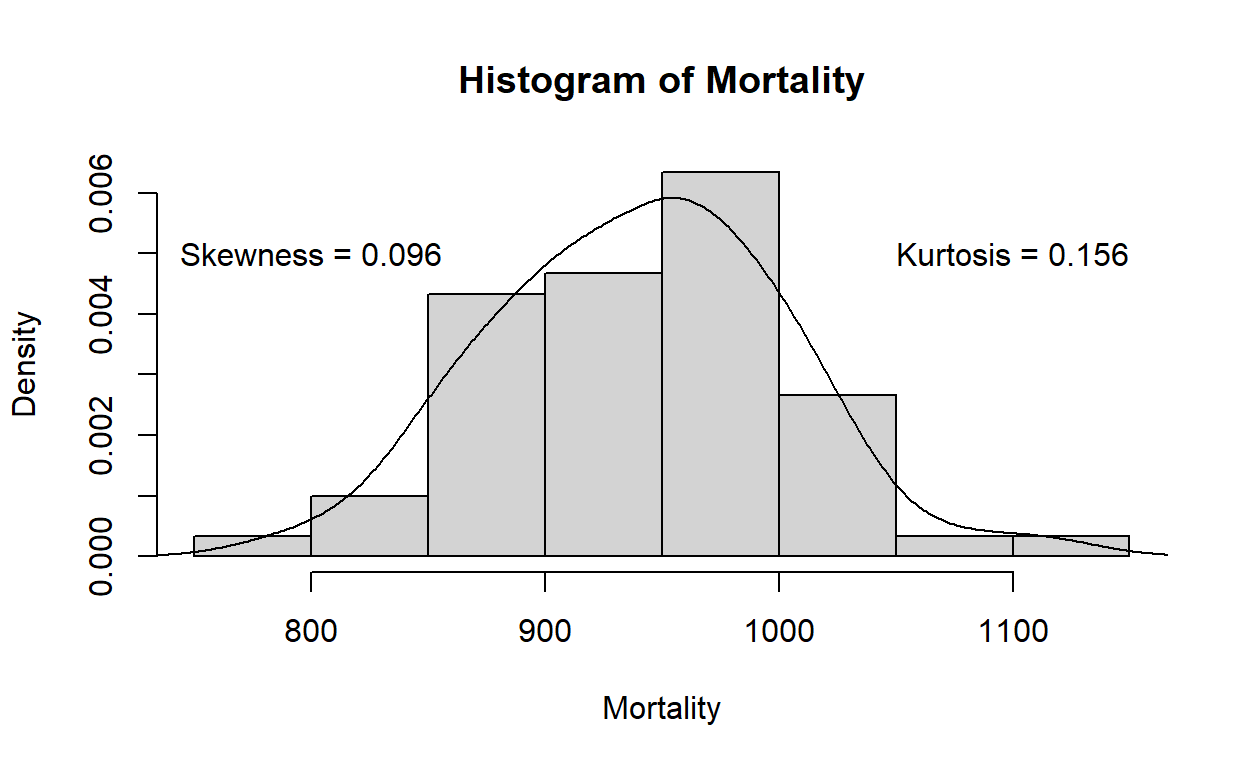
skewness(Mortality)

Skewness |    SE
----------------
   0.096 | 0.301
kurtosis(Mortality)

Kurtosis |    SE
----------------
   0.156 | 0.559
hist(Mortality,freq = F)
lines(density(Mortality))
text(x= 800, y=0.005, label= "Skewness = 0.096")
text(x= 1100, y=0.005, label= "Kurtosis = 0.156")

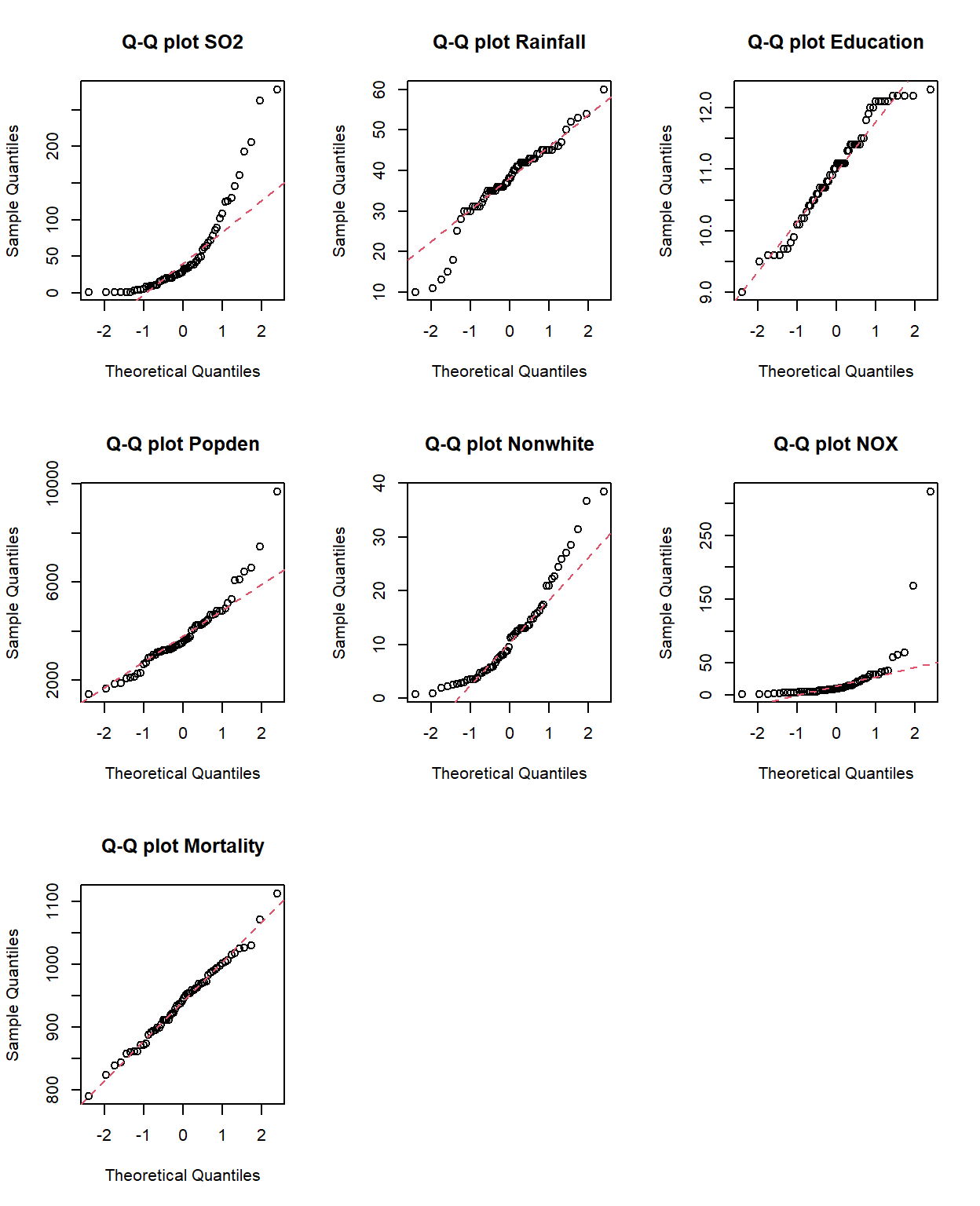
QQplots

par(mfrow=c(3,3))                                                 
qqnorm(SO2, main="Q-Q plot SO2"); qqline(SO2, col = 2, lty = 2)
qqnorm(Rainfall, main="Q-Q plot Rainfall"); qqline(Rainfall, col = 2, lty = 2)
qqnorm(Education, main="Q-Q plot Education"); qqline(Education, col = 2, lty = 2)
qqnorm(Popden, main="Q-Q plot Popden"); qqline(Popden, col = 2, lty = 2)
qqnorm(Nonwhite, main="Q-Q plot Nonwhite"); qqline(Nonwhite, col = 2, lty = 2)
qqnorm(NOX, main="Q-Q plot NOX"); qqline(NOX, col = 2, lty = 2)
qqnorm(Mortality, main="Q-Q plot Mortality"); qqline(Mortality, col = 2, lty = 2)

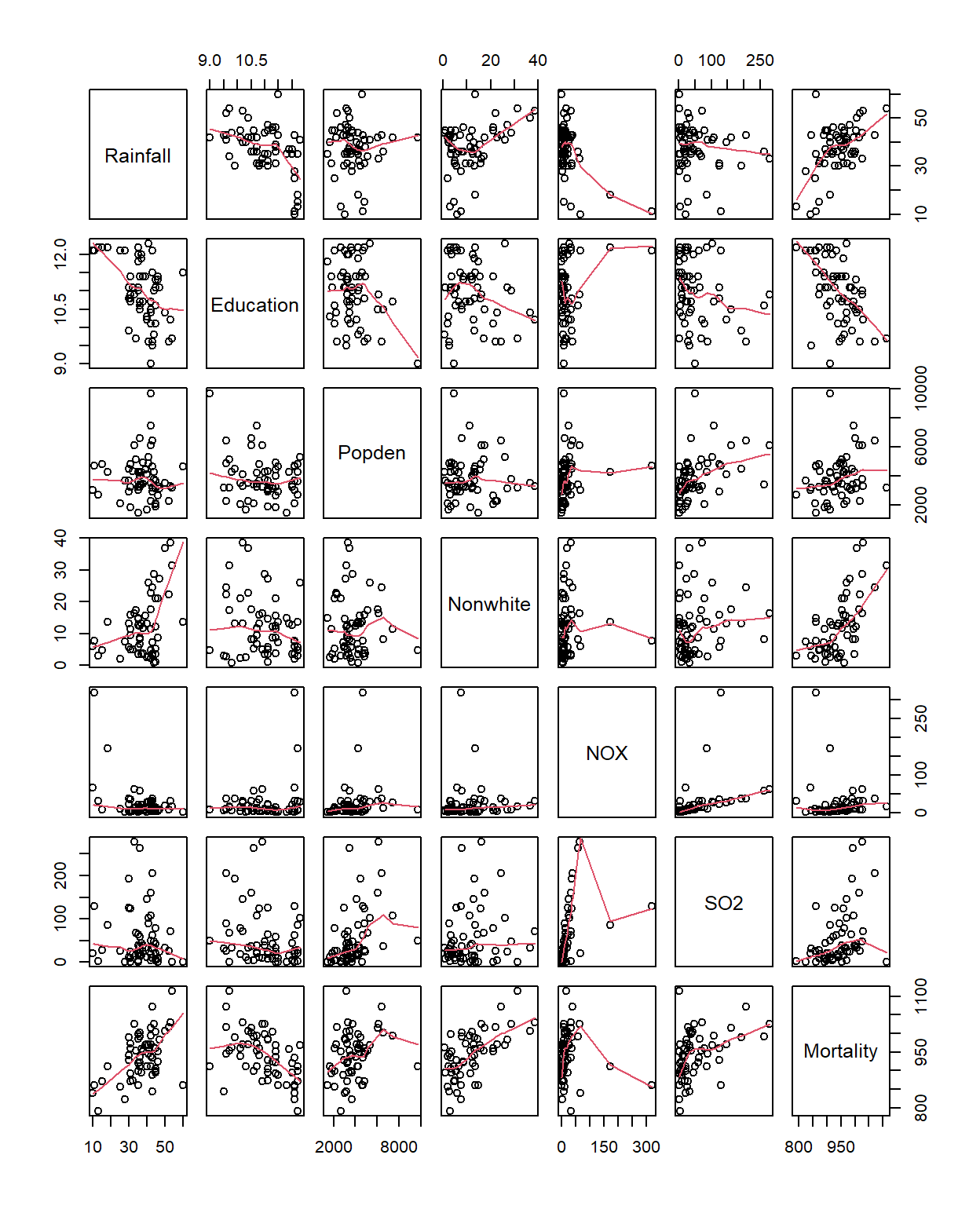
Relaciones bivariadas

Veamos que relación hay entre las distintas variables. Aquí utilizo una función smoooth (regresión con pesos locales) que permite sugerir con los propios datos que tipo de relación pudieran tener.

pairs(airpoll, panel=panel.smooth)

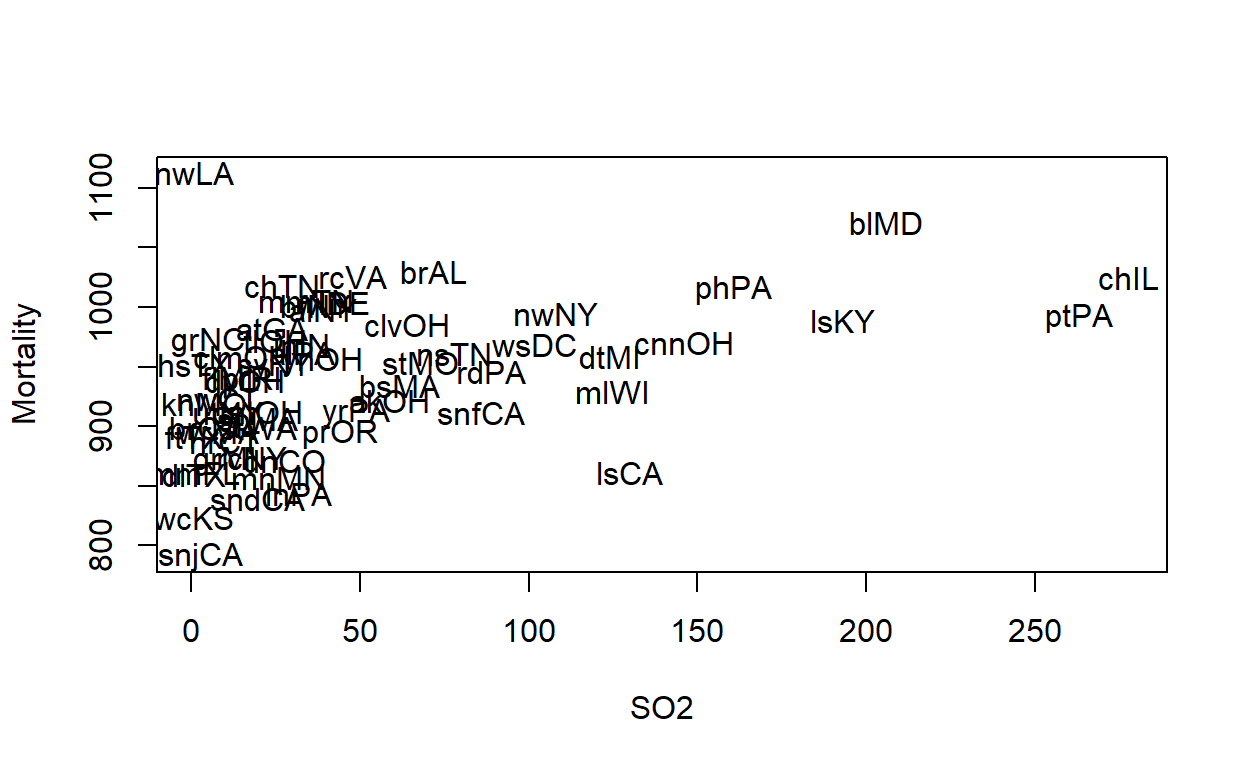
veamos con mas detalle la relación SO2-mortalidad

nombres<-abbreviate(row.names(airpoll))
par(mfrow=c(1,1))
plot(SO2,Mortality,lwd=2,type="n")
text(SO2,Mortality,labels=nombres,lwd=2)


detach(airpoll)

C.1

R.2 valores faltantes

airpoldf <- read.table("datofalta.txt")
airpoldf
attach(airpoldf)

Lo mas fácil la media

summary(Mortality)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
  789.7   892.4   943.7   936.6   977.1  1112.0       1 
sum(is.na(Mortality))

[1] 1

Cual es el valor imputado? Cuales son los problemas asociados a esta imputación?

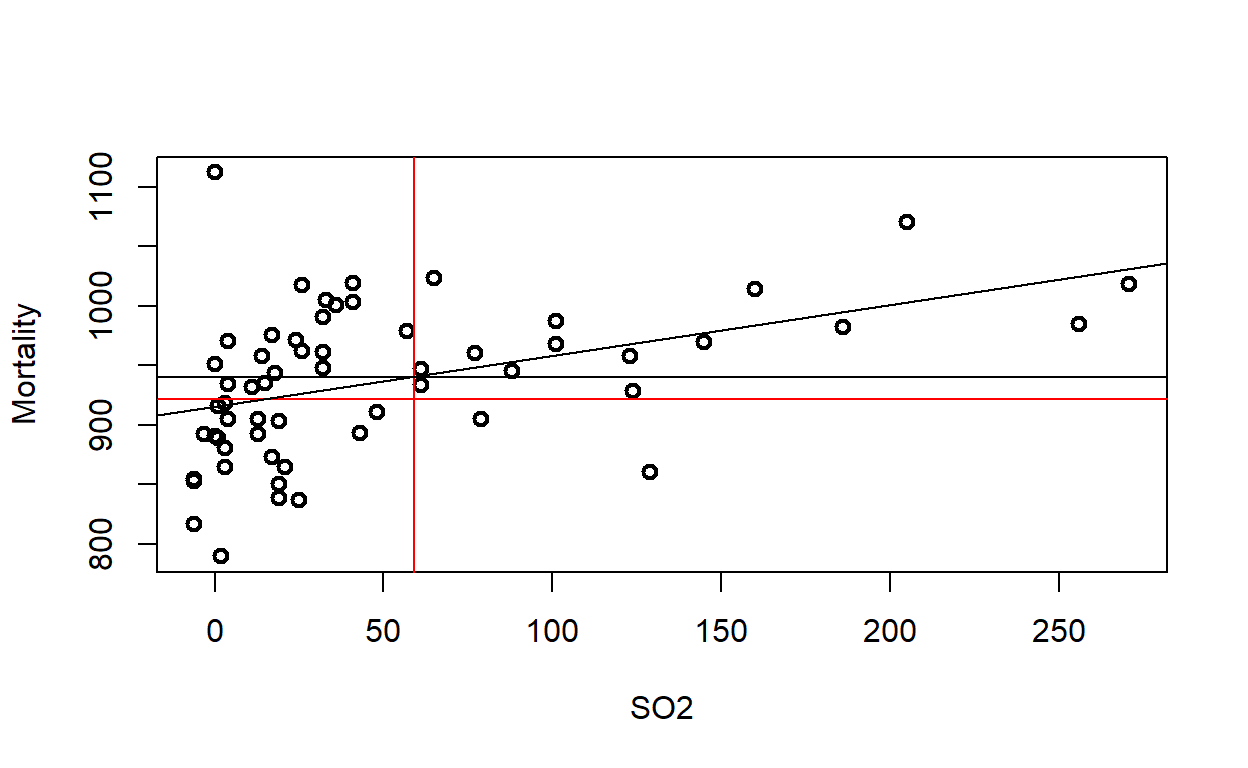
regresión mortalidad y SO2

par(mfrow=c(1,1)) 
plot(SO2,Mortality,lwd=2)
abline(v = 59, h = 940.2)
abline(v = 59, h = 921.9, col = "red")


regmort<-lm(Mortality~SO2)
summary(regmort)


Call:
lm(formula = Mortality ~ SO2)

Residuals:
     Min       1Q   Median       3Q      Max 
-126.625  -38.213   -7.796   35.582  196.528 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 915.4721     9.4932  96.435  < 2e-16 ***
SO2           0.4266     0.1177   3.624  0.00062 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 57.47 on 57 degrees of freedom
  (1 observation deleted due to missingness)
Multiple R-squared:  0.1872,    Adjusted R-squared:  0.173 
F-statistic: 13.13 on 1 and 57 DF,  p-value: 0.0006196
m <-  (915.4720997 + (0.4266209*59))  

par(mfrow=c(1,1)) 
plot(SO2,Mortality,lwd=2)
abline(v = 59, h = 940.2)
abline(v = 59, h = 921.9, col = "red")
abline(lm(Mortality~SO2))


predict(regmort, list(SO2=58)) 

       1 
940.2161 
logM<-log(Mortality)
logSO2<-log(SO2+7)
loglog<-lm(logM~logSO2)
summary(loglog)


Call:
lm(formula = logM ~ logSO2)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.136793 -0.030759  0.000398  0.029763  0.212163 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.749926   0.021463 314.487  < 2e-16 ***
logSO2      0.026633   0.005928   4.493 3.48e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.05863 on 57 degrees of freedom
  (1 observation deleted due to missingness)
Multiple R-squared:  0.2615,    Adjusted R-squared:  0.2486 
F-statistic: 20.19 on 1 and 57 DF,  p-value: 3.482e-05
par(mfrow=c(1,2))
plot(SO2,Mortality,lwd=2) 
abline(regmort)
abline(v = 58, h = c(940.2161, 954.4211), col = "red")
      
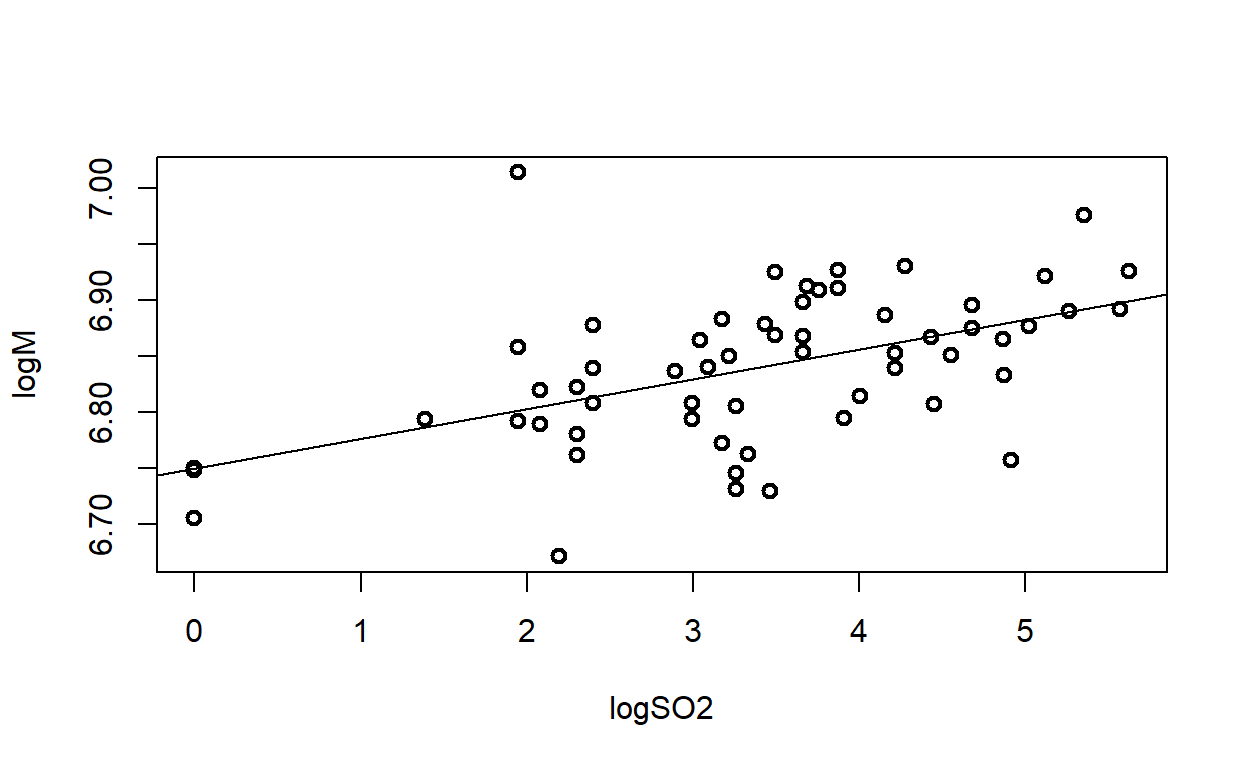
plot(logSO2,logM,lwd=2) 
abline(lm(logM~logSO2))
abline(v = 58, h = 940.2161, col = "red")


plot(logSO2,logM,lwd=2) 
abline(lm(logM~logSO2))

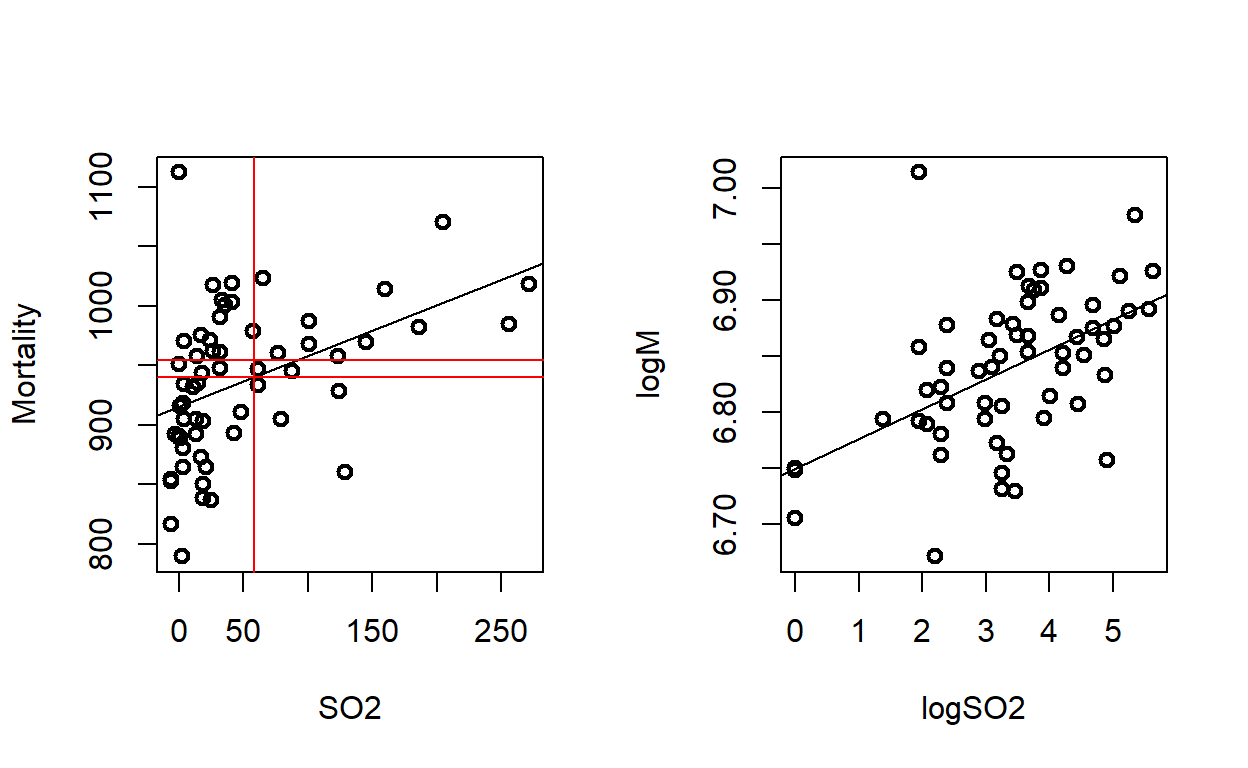
el valor de SO2 que corresponde al valor faltante de mortalidad es 58. Como hemos generado un modelo de logaritmos a ambos lados de la ecuación sacamos el log del (SO2+7)

log(58+7)

[1] 4.174387

Usamos la función predict para predecir el valor correspondiente de Mortalidad

predict(loglog, list(logSO2=4.174387)) 

       1 
6.861105

pero recordando que usamos logaritmos en el modelo, retrotransformamos con el antilog con base e (e elevado al numero que nos interesa retro transformar)

exp(6.861105)

[1] 954.4211

El valor predicho por regresión lineal es? Cuales son los problemas asociados a esta imputación?

Fin

Patil, Indrajeet, Dominique Makowski, Mattan S. Ben-Shachar, Brenton M. Wiernik, Etienne Bacher, and Daniel Lüdecke. 2022. “Datawizard: An r Package for Easy Data Preparation and Statistical Transformations” 7: 4684. https://doi.org/10.21105/joss.04684.

References