NOTA: Para descargar los datos, dar click en el boton. Aparece una pantalla con los datos, luego dar click derecho y poner guardar como (save as). Guardar el txt donde van a trabajar

R.1

Vamos a ver una serie de datos para ver si existe una relación lineal entre ellos.

data<-read.table("twosample.txt",header=T)
attach(data)
data

plot(x,y)

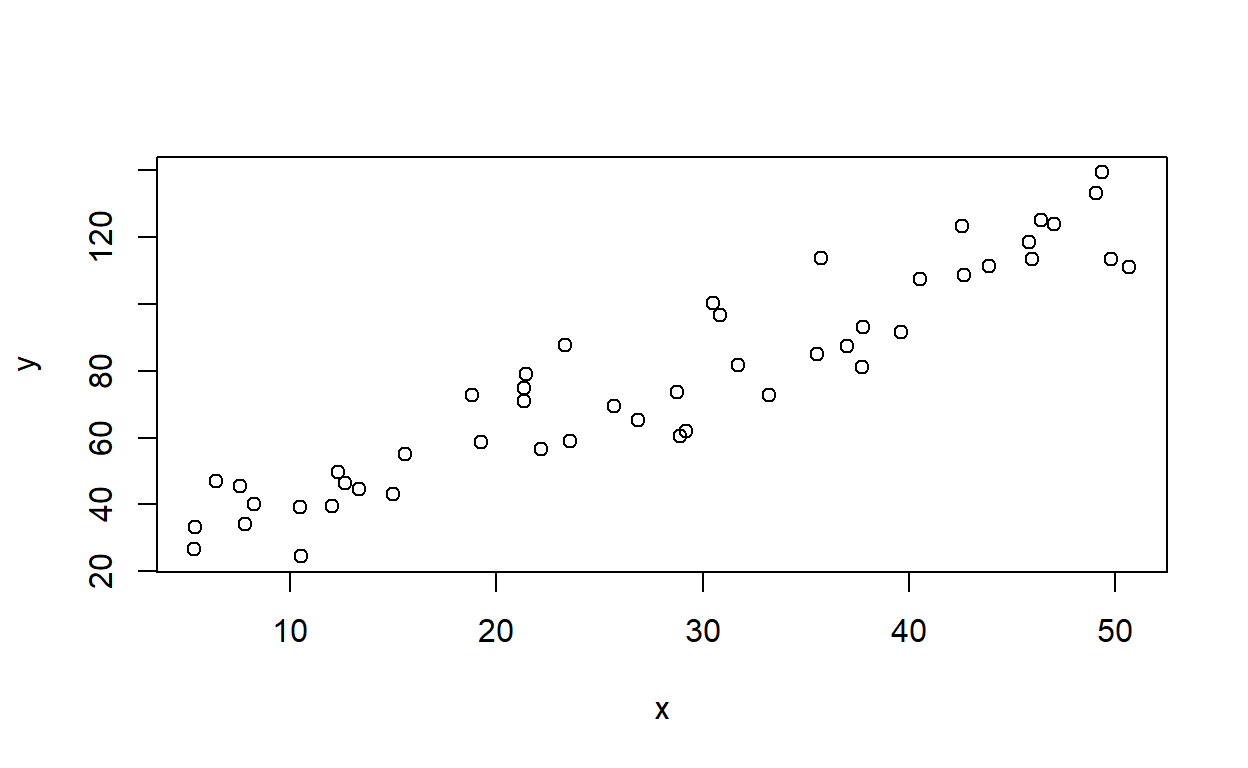
Se acuerdan que necesitamos primero para calcular el coeficiente de correlación de pearson? Las varianzas individuales

var(x)

[1] 199.9837

var(y)

[1] 977.0153

¿y que más? La covarianza y estamos hechos

var(x,y)

[1] 414.9603

Ahora calculamos r

var(x,y)/sqrt(var(x)*var(y))

[1] 0.9387684

Ahora hagamoslo en automático

cor(x,y)

[1] 0.9387684

Y ahora hagamos la prueba de hipótesis

Calculamos EE de r

EEr<-((1-(cor(x,y)^2))/(length(x)-2))^0.5
EEr

[1] 0.05025759

Calculo t de la muestra

te<-cor(x,y)/EEr
te

[1] 18.67914

Calculo t de tablas

qt(0.975,47)

[1] 2.011741

Calculo la p

2*(1-pt(18.67914,47))

[1] 0

Ahora hagamoslo de manera automática

pearson<-cor.test(x,y)
pearson


    Pearson's product-moment correlation

data:  x and y
t = 18.679, df = 47, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.8934139 0.9651786
sample estimates:
      cor 
0.9387684

¿Que nos falta?. Pues no sabemos si cumplimos con los supuestos. Veamos el de normalidad

par(mfrow=c(1,2))
qqnorm(x, main="Q-Q plot x"); qqline(x, col = 2, lty = 2)
qqnorm(y, main="Q-Q plot y"); qqline(y, col = 2, lty = 2)

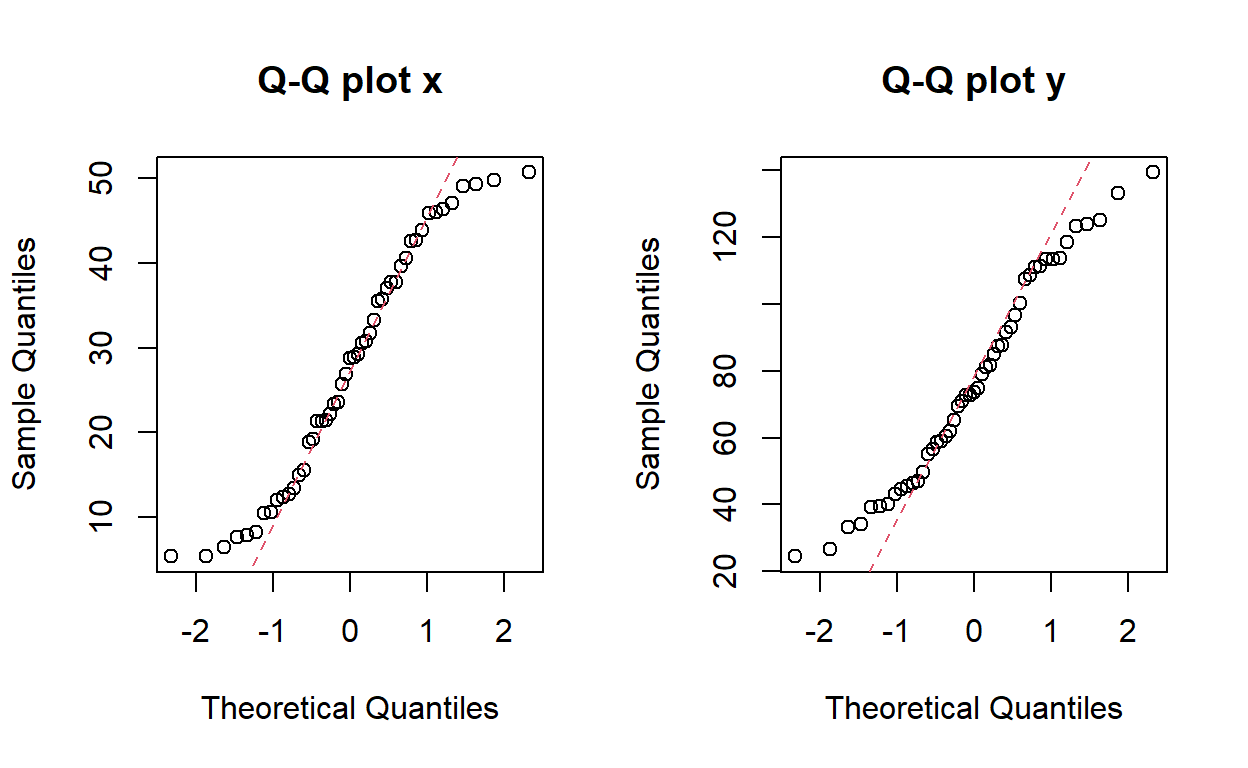
¿Que opciones tengo?.

Hacer una prueba de sesgo y kurtosis para ver si estas desviaciones son significativas
Si son significativas, puedo intentar transformaciones o puedo utilizar muchas de las otras pruebas de correlación que son robustas a la violación de este supuesto. Vean Q y k p.76 y Crawley p.97-102.

Script Correlación

R.1

Fin