NOTA: Para descargar los datos, dar click en el boton. Aparece una pantalla con los datos, luego dar click derecho y poner guardar como (save as). Guardar el txt donde van a trabajar

R.3

Volvamos al ejemplo de las concentraciones de ozono en los invernaderos y vamos a preguntarnos si el promedio de sus concentraciones de ozono es significativamente distinto

ozono<-read.table("gardens.txt",header=T)
attach(ozono)
names(ozono)

Veamos un gráfico

ozonoAB<-c(gardenA,gardenB)
ozonoAB

 [1] 3 4 4 3 2 3 1 3 5 2 5 5 6 7 4 4 3 5 6 5

etiqueta<-factor(c(rep("A",10),rep("B",10)))
etiqueta

 [1] A A A A A A A A A A B B B B B B B B B B
Levels: A B

boxplot(ozonoAB~ etiqueta, notch=T,
        xlab="Invernadero",ylab="Ozono")

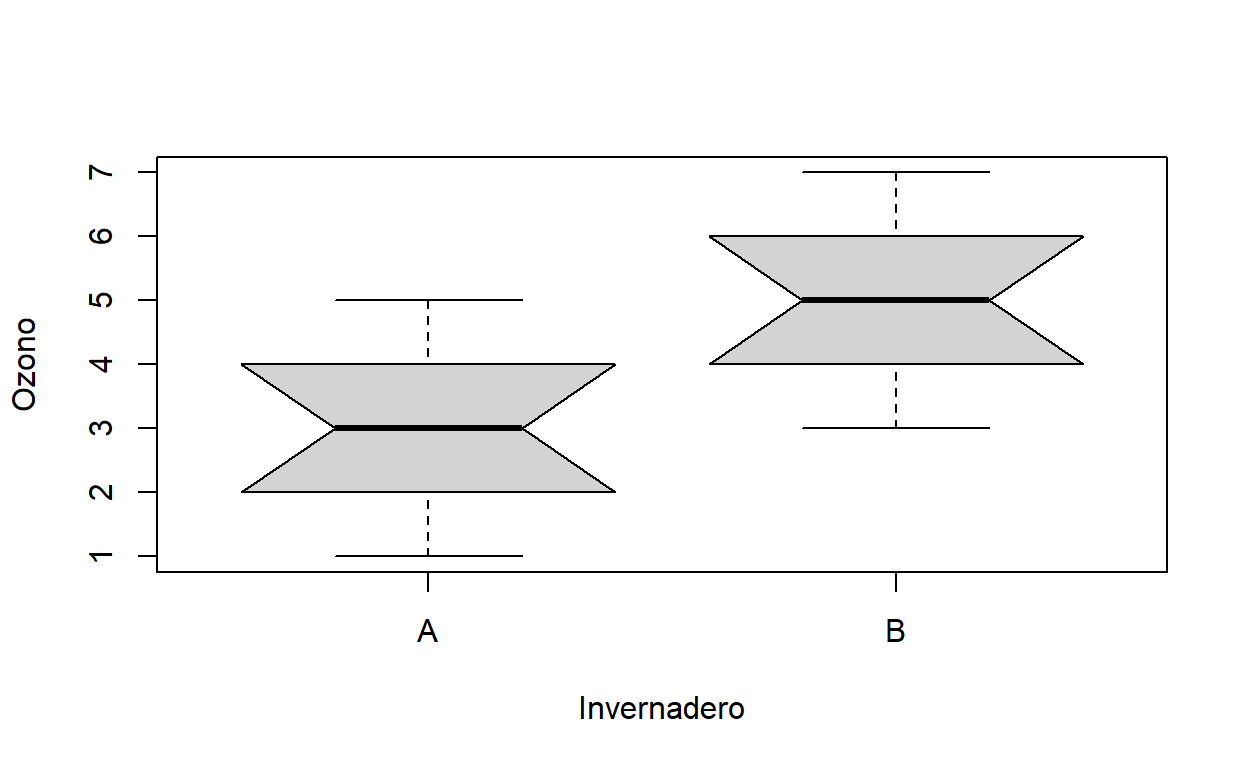
Si usamos el ojimetro, parece ser que no sus medianas no son distintas porque los intervalos intercuartil no se sobrelapan. Ahora hagamos una prueba de t (para comparar las medias) a pie.

¿Que necesitamos?

los grados de libertad. dijimos que para una prueba de dos poblaciones calculamos el total de observaciones (20) menos el num. de parámetros estimados antes de realizar la prueba (dos medias). Así que tenemos 18 g.l.
Necesitamos calcualar las varianzas individuales de cada invernadero, para poder calcular la diferencia de EE.

s2A<-var(gardenA)
s2B<-var(gardenB)

¿Luego que sigue?

Calculamos la t de student para la diferencia de medias

(mean(gardenA)-mean(gardenB))/sqrt(s2A/10+s2B/10)

[1] -3.872983

Noten que podemos ignorar el signo de la t. Porque solo depende que cual media pusimos primero. El valor absoluto es lo que importa.

Ahora necesitamos el valor crítico de la distribución de t de referencia para determinar si aceptamos o rechazamos la hipótesis de que no hay diferenicas entre medias (que vienen de la misma población). Se trata de un problema de una o dos colas?

Como no me interesa cual es mayor o menor, ni tengo ninguna hipótesis de que invernadero debía tener mas o menos ozono, entonces es de dos colas, por lo tanto uso una probabilidad de?

qt(0.975,18)

[1] 2.100922

¿Acepto o rechazo la hipótesis de que son iguales?

En virtud de que el valor calculado es mayor que el valor crítico se rechaza la hipótesis nula. (recuerden más alto=rechazo Ho más bajo=acepto)

Finalmente necesito saber cual es la probabilidad de que encuentre yo la diferencia entre estas dos muestras (o una más extrema) a pesar de que provienen de poblaciones con la misma media. Recuerden que es un problema de dos colas y por esa razón necesito calcular pt y después multiplicarlos por dos (para los dos extremos).

p<-2*pt(-3.872983,18)
p

[1] 0.00111454

para calcular los intervalos de confianza para la diferencia medias

difmed<-mean(gardenA)-mean(gardenB)
EEdifmed<-sqrt(s2A/10+s2B/10)
t.de.tablas.alfa.05.gl.18<-qt(0.975,18)
t.de.tablas.alfa.05.gl.18

[1] 2.100922

IC95<-(EEdifmed)*(t.de.tablas.alfa.05.gl.18)
Cotasup<- difmed+IC95
Cotasup

[1] -0.9150885

Cotainf<- difmed-IC95 
Cotainf

[1] -3.084911

IC95t<-(sqrt(s2A/10+s2B/10))*(qt(0.975,18))
  IC95t

[1] 1.084911

¿Cual es la probabilidad de que suceda? Ahora el automático

pruebat<-t.test(gardenA,gardenB)
pruebat


    Welch Two Sample t-test

data:  gardenA and gardenB
t = -3.873, df = 18, p-value = 0.001115
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -3.0849115 -0.9150885
sample estimates:
mean of x mean of y 
        3         5

Entonces reporto la concentración de ozono fue significativamente más alta en el invernadero B (5.0 ppm) que en el A(3.0ppm; t=3.87, p=0.001(dos colas), gl=18)

Ahora, pudiéramos tener el problema de que las varianzas no son iguales. entonces antes de hacer una prueba de t, necesitamos preguntarnos si las varianzas son significativamente distintas. Comparemos las de los invernaderos B y C.

var(gardenB)

[1] 1.333333

var(gardenC)

[1] 14.22222

¿Se acuerdan que la distribución de F era la adecuada para comparar varianzas? la pregunta es, ¿cual es la probabilidad de que estas dos muestras hayan sido sacada de poblaciones que tienen la misma varianza? El valor de F es simplemente el cociente de las varianzas

CocienteF<-var(gardenC)/var(gardenB)
CocienteF

[1] 10.66667

Ahora comparo con la distribución de probabilidad de F para los grados de libertad correspondientes, y como no tengo ninguna idea de cual de las muestras debiera tener una varianza más alta, entonces es una prueba de dos colas.

Como F no es simétrica, necesito calcular ambos lados.

qf(0.975,9,9)

[1] 4.025994

qf(0.025,9,9)

[1] 0.2483859

¿Que concluyo?

¿Cual es la probabilidad de que estas dos muestras provengan de poblaciones con la misma varianza?

2*(1-pf(CocienteF,9,9))

[1] 0.001624199

Ahora el automático

var.test(gardenB,gardenC)


    F test to compare two variances

data:  gardenB and gardenC
F = 0.09375, num df = 9, denom df = 9, p-value = 0.001624
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.02328617 0.37743695
sample estimates:
ratio of variances 
           0.09375

Ahora, si encontráramos que suponer que las poblaciones de las que provienen las muestras no se distribuyen de manera normal entonces tenemos la alternativa de la prueba de Wilcoxon de suma de rangos. Esta es idéntica en su sistema a la de los rangos signados. Veamos como

Lo primero que hago es poner todas las observaciones en un mismo vector

ozone<-c(gardenA,gardenB)
ozone

 [1] 3 4 4 3 2 3 1 3 5 2 5 5 6 7 4 4 3 5 6 5

Ahora les hago sus etiquetas para que no se me pierdan

etiqueta<-c(rep("A",10),rep("B",10))
etiqueta

 [1] "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "B" "B" "B" "B" "B" "B"
[17] "B" "B" "B" "B"

Ahora hago un vector de los rangos con la función rank

rangoscomb<-rank(ozone)
rangoscomb

 [1]  6.0 10.5 10.5  6.0  2.5  6.0  1.0  6.0 15.0  2.5 15.0 15.0 18.5
[14] 20.0 10.5 10.5  6.0 15.0 18.5 15.0

Noten que para todos los valores repetidos se hace un promedio de los rangos que les tocan.

tapply(rangoscomb,etiqueta,sum)

  A   B 
 66 144

Finalmente uso el valor más pequeño (66) para compararlo con el valor de tablas para el etadístico W para n de 10 y 10 y un alfa del 5% (W=78). Como nuestro valor es menor (porque uso como referencia el mas pequeño del par que obtuve), entonces rechazo mi H0. Las Medias son significativamente distintas.

Ahora el automático.

wilcox.test(gardenA,gardenB)


    Wilcoxon rank sum test with continuity correction

data:  gardenA and gardenB
W = 11, p-value = 0.002988
alternative hypothesis: true location shift is not equal to 0

Las diferencias se deben a que R utiliza un algoritmo de aproximación para calcular valores de z. Es ligeramente distinto del tradicional que hicimos arriba. La mecánica es la misma. Noten la diferencia en las p de t y W. Wilcoxon es menos poderoso (95%). Pero es el correcto si las distribuciones son sesgadas. También es correcto si no lo son (aunque poco menos poderoso). t no es correcta si hay desviaciones sustanciales de la normalidad.

Script Prueba de hipótesis de dos poblaciones

R.3

Fin