Script Estimación 1 - El papel de la probabilidad

El teorema de tendencia central

R.1

Pidámosle a R que tome 10000 números al azar (0-10) y que grafique con que frecuencia eligió cada número ¿que esperan ver?

numeros<-(runif(10000)*10)

hist(runif(10000)*10,main="")

Tomemos 5 números al azar del 0 al 10 y saquemos el promedio de los cinco números ¿cual creen que sea el promedio típico? Hagámonos

clase<-c((mean(,,,,)), (mean(,,,,)))
clase

Ahora pidámosle a R que lo haga 10000 veces (¡10000 muestras de números del 0 al 10!)

means<-numeric(10000)
for (i in 0:10000){ 
  means[i]<- mean(runif(5)*10)}
  
hist(means,ylim=c(0,1600))

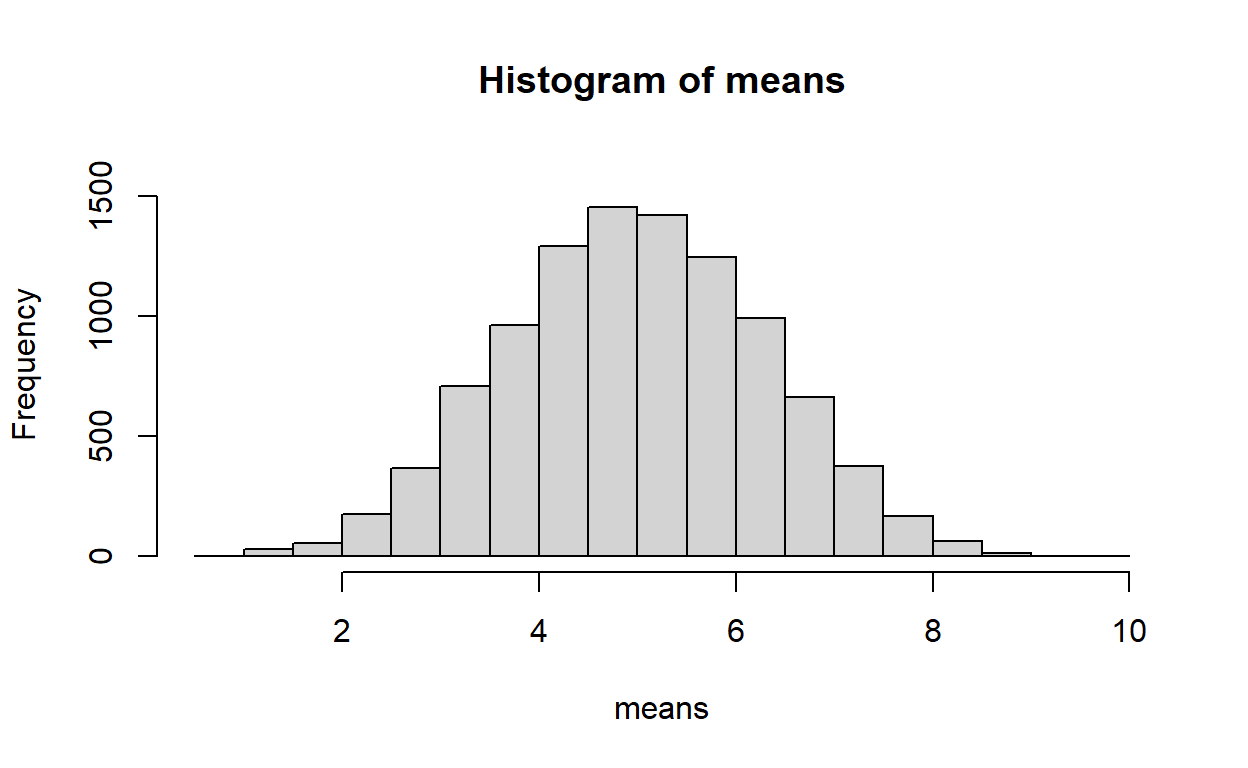
Noten que existe una tendencia central. Lo que significa que el mero hecho de muestrear genera una tendencia central en el valor promedio.

C.1

R.2

El histograma de los números se ve como una distribución normal. ¿porque no dibujamos una función normal sobre este histograma para ver que tan normal es? ¿Que necesitamos saber?

mean(means)

[1] 4.992107
sd(means)

[1] 1.3046

y meterlo en la ecuación \[ f(y) = \frac{1/}{(\sqrt{2 \pi} \sigma)} e^{y- \mu / 2 \sigma^2} \] para cada valor de means verdad? R lo hace por ustedes

Primero generamos una serie de números para el eje x que le permita a R saber cada cuando poner un puntito de la línea. Si queremos una linea suave una buena regla es 100 números. Como queremos números entre 0 y 10:

xv<-seq(0,10,0.1)

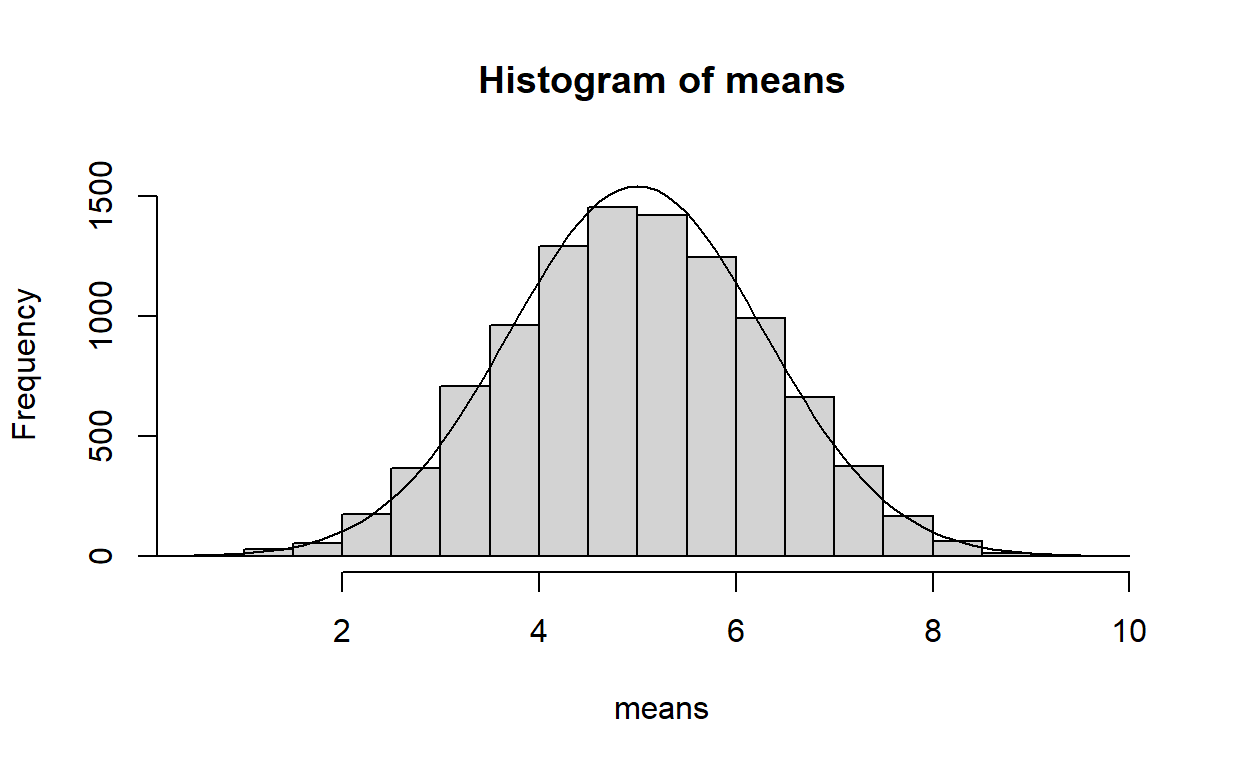
Como la función normal tiene un área bajo la curva de 1 y nosotros tenemos 10000 valores, necesitamos escalar la curva multiplicándola por el número de valores que se encuentran de cada lado de el valor de en medio (mediana).

yv<-dnorm(xv,mean=4.993275,sd=1.291482)*5000

hist(means,ylim=c(0,1600))
lines(xv,yv)

El ajuste es perfecto! Lo interesante del teorema de tendencia central es que no importa cual sea la distribución real, si se toma una muestra de ella, se comportará normalmente.

C.2

R.3

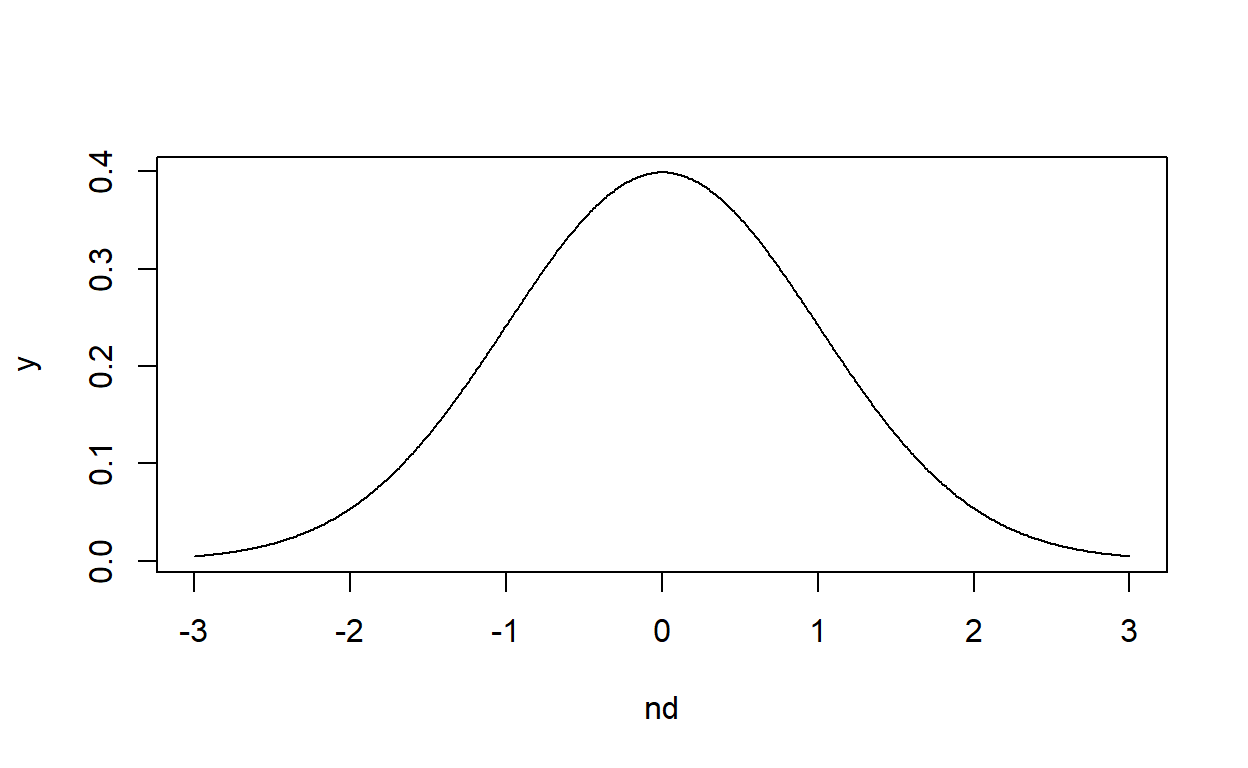
El estandarizar la curva normal tiene muchas ventajas. Nos permite por ejemplo saber cual es el área hasta cualquier valor del eje X (llamados desviaciones estándar).

Pidámosle a R que nos dibuje una Distribución Normal Estandarizada. Recuerden que lo primero que hay que hacer cuando se dibujan líneas

nd<-seq(-3,3,0.01)

Cuando no le damos la media y a la var, significa que queremos la estandarizada (el default), solo le dimos las x.

y<-dnorm(nd)
plot(nd,y,type="l")

Ahora utilicemos pnorm para determinar que proporción de valores caen por debajo de dos desviaciones estándar.

pnorm(-2)

[1] 0.02275013

que proporción? y ahora por debajo de 1 ds

pnorm(-1)

[1] 0.1586553

¿Que pasa si queremos saber que proporción de muestras caen A LA DERECHA de la desviación 3?

esta es una opción

 1-pnorm(3)

[1] 0.001349898

¿y la otra?

pnorm(-3)

[1] 0.001349898

Es claro que un valor de 3 cuando la media es 0 en una dn es muy poco probable (0.13% de las veces cuando se saca una muestra de la pob.)

Ahora veamos un uso muy común de la distribución de z. Este es preguntarse bajo una situación aleatoria (solo por el hecho de muestrear una población) entre que desviaciones estándar podemos encontrar el 95% de las muestras. (noten que al ser simétrica, tenemos que alojar 2.5% de los casos “excedentes” de cada lado y para ello definimos un vector dentro de la funció qnorm (cuantiles normales)

qnorm(c(0.025,0.975))

[1] -1.959964  1.959964

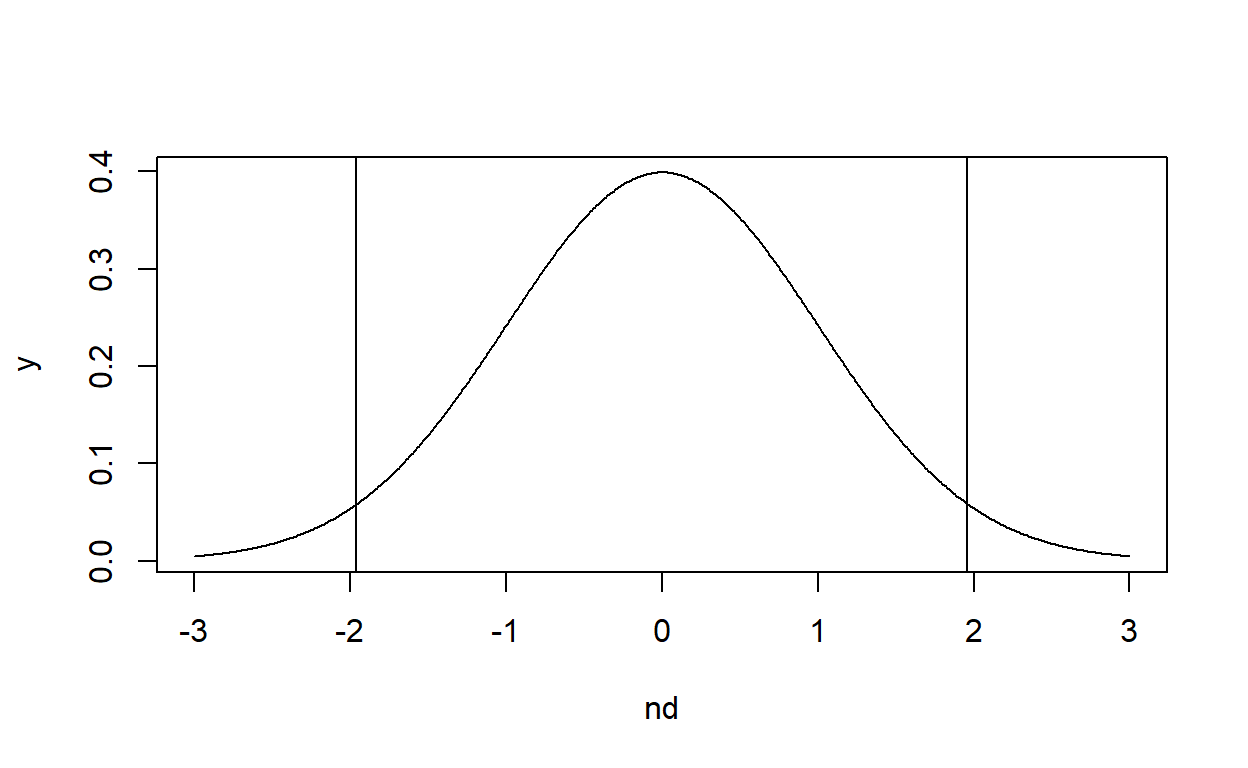
ahora dibujémoslo

y<-dnorm(nd)

plot(nd,y,type="l")
  abline(v=-1.96)
  abline(v=+1.96)

Esto es muy importante porque si encontramos que nuestro muestreo no se ajusta a estos valores esperados entonces posiblemente pertenezcan a dos poblaciones distintas. Este es el principio básico de todas las pruebas de significancia (p=0.05), el origen de el error estándar (1.96 desv. estándar), los límites de confianza etc.

Tarea de hoy

Supongamos que tenemos una muestra de 100 colibríes de una especie A. Les hemos medido la extensión de alas y encontramos que la media es 17 cm y la desviación estándar es de 0.8 cm.

  1. Dibujen la distribución de probabilidad bajo un supuesto de normalidad

  2. ¿que probabilidad hay de encontrar un caso con una extensión mayor a 18cm?

Noten que cualquier valor de y en una distribución normal se puede convertir en un valor de z. Recuerden que \(z=(y-media(y))/desv.stand\).

  1. ¿y la de encontrar un ave con una extensión menor a 15?

  2. ¿ustedes creen que un ave con una extensión de 15cm puede decirse que con una confianza del 95% pertenece a la misma población?

  3. ¿entre que medidas de extensión de alas se puede decir con un 95% de confianza que las aves pertenecen a esa población?

¡Fin!