NOTA: Para descargar los datos, dar click en el boton. Aparece una pantalla con los datos, luego dar click derecho y poner guardar como (save as). Guardar el txt donde van a trabajar

R.1

Estimación de parámetros de tendencia central

Sabemos que aunque los datos no se agrupen alrededor de un valor típico si hacemos muestras consecutivas los estadísticos de estas van a tener una tendencia central.

Veamos un cuerpo de datos. Una variable y.

yvals <- read.table("yvalues.txt",header=T)
attach(yvals)
yvals

Una manera muy simple de medir la tendencia central es ver cual es el valor más frecuente. Este se denomina MODA

yord<-sort(y)
yord

 [1] 1.029680 1.032829 1.037292 1.053150 1.053251 1.063707 1.064455
 [8] 1.070355 1.071217 1.075693 1.081053 1.084013 1.086288 1.094628
[15] 1.095193 1.100543 1.101244 1.102617 1.104005 1.108847 1.108853
[22] 1.109046 1.110171 1.112230 1.117421 1.120611 1.121111 1.126974
[29] 1.127780 1.128891 1.130020 1.130521 1.134060 1.145682 1.149131
[36] 1.150670 1.154751 1.156906 1.190229

#windows()
hist(y)

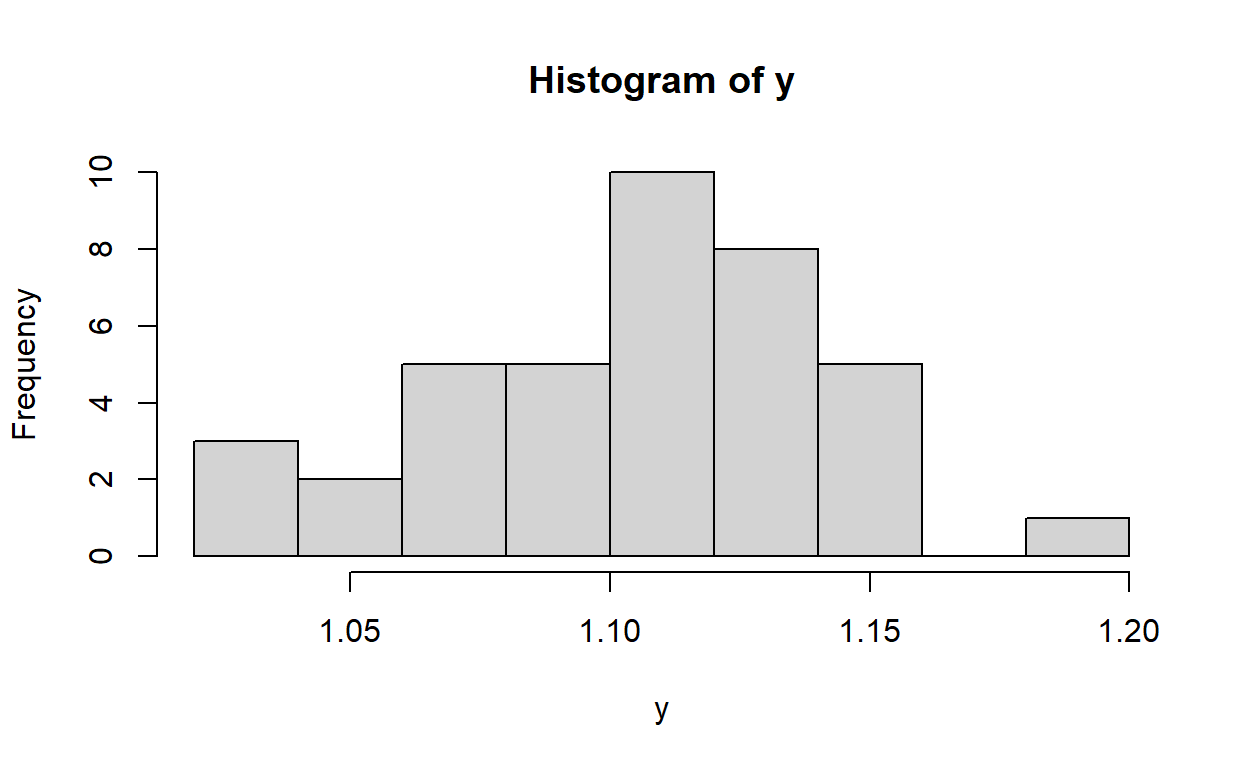
¿cual es la clase modal aquí?

Pero ahora queremos saber la media aritmética (el promedio) que es la suma de todos los valores dividido por n. ¿Que hago?

total<-sum(y)
sum(y)

[1] 43.03511

pero ahora necesito saber cuantos valores son

n<-length(y)
n

[1] 39

media<- total/n
media

[1] 1.103464

pero ahora quiero tener una función que me sirva para siempre

media.aritmetica <- function(x) {
  sum(x)/length(x) }

ya está, ahora probémosla

data<-c(3,4,6,7)
media.aritmetica(data)

[1] 5

media.aritmetica(y)

[1] 1.103464

¡Que bien! ¡R es fantástico! puedo calcular la media siempre que me plazca.

En realidad la mayor parte de las funciones estadísticas están ya construidas en R. Por supuesto que la media es una de ellas. Solo quería mostrarles que no hay nada obscuro detrás de los objetos ya creados en R

mean(y)

[1] 1.103464

La media como medida de tendencia central tiene el serio problema de que es muy sensible a valores atípicos. vean lo siguiente.

dataat<-c(data,100)
dataat

[1]   3   4   6   7 100

mean(dataat)

[1] 24

comparado con

mean(data)

[1] 5

Una alternativa es la mediana, que es el valor de en medio, una vez que todos los valores han sido ordenados. Veamos dataat

dataat

[1]   3   4   6   7 100

¿Cual es la mediana?

median(dataat)

[1] 6

es mucho mejor estimación de el centro que 24.

¿y de data?

data

[1] 3 4 6 7

median(data)

[1] 5

¿ y para y?

median(y)

[1] 1.108847

mean(y)

[1] 1.103464

Se parecen mucho porque no hay valores atípicos y porque la distribución es simétrica.

Ahora pensemos en fenómenos que cambian multiplicativamente. ¿Conocen alguno?

Uno de los más comunes en ecología es el crecimiento poblacional y por lo tanto la dispersión de organismos de una población. En dichos casos la media aritmética y/o la mediana suelen ser pésimos estimadores de la tendencia central. Veamos un ejemplo.

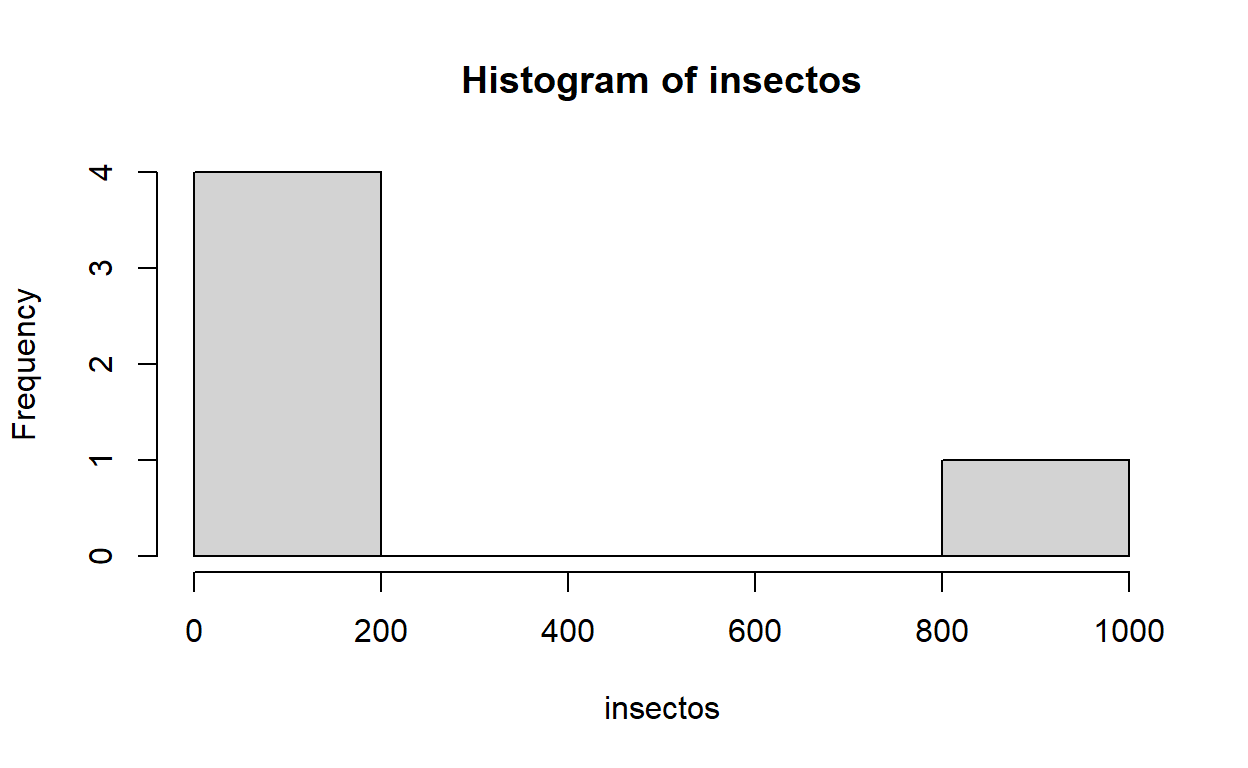
El número de insectos en una serie de plantas vecinas es

insectos<-c(1,10,1000,10,1)

¿Cual es la mejor estimación de tendencia central?

#windows()
hist(insectos)

mean(insectos)

[1] 204.4

median(insectos)

[1] 10

C.1

R.2

Lo que se usa es la media geométrica que si se acuerdan hay dos maneras de calcularla. Para el ejemplo de los insectos ¿cual es la mas simple?

100000^0.2

[1] 10

¿y la otra?

exp(mean(log(insectos)))

[1] 10

detach(yvals)
rm(insectos)
ls()

[1] "data"             "dataat"           "media"           
[4] "media.aritmetica" "n"                "total"           
[7] "yord"             "yvals"

C.2

R.3 Medidas de dispersión

Veamos un cuerpo de datos cualquiera y preguntémonos cómo podemos medir su dispersión.

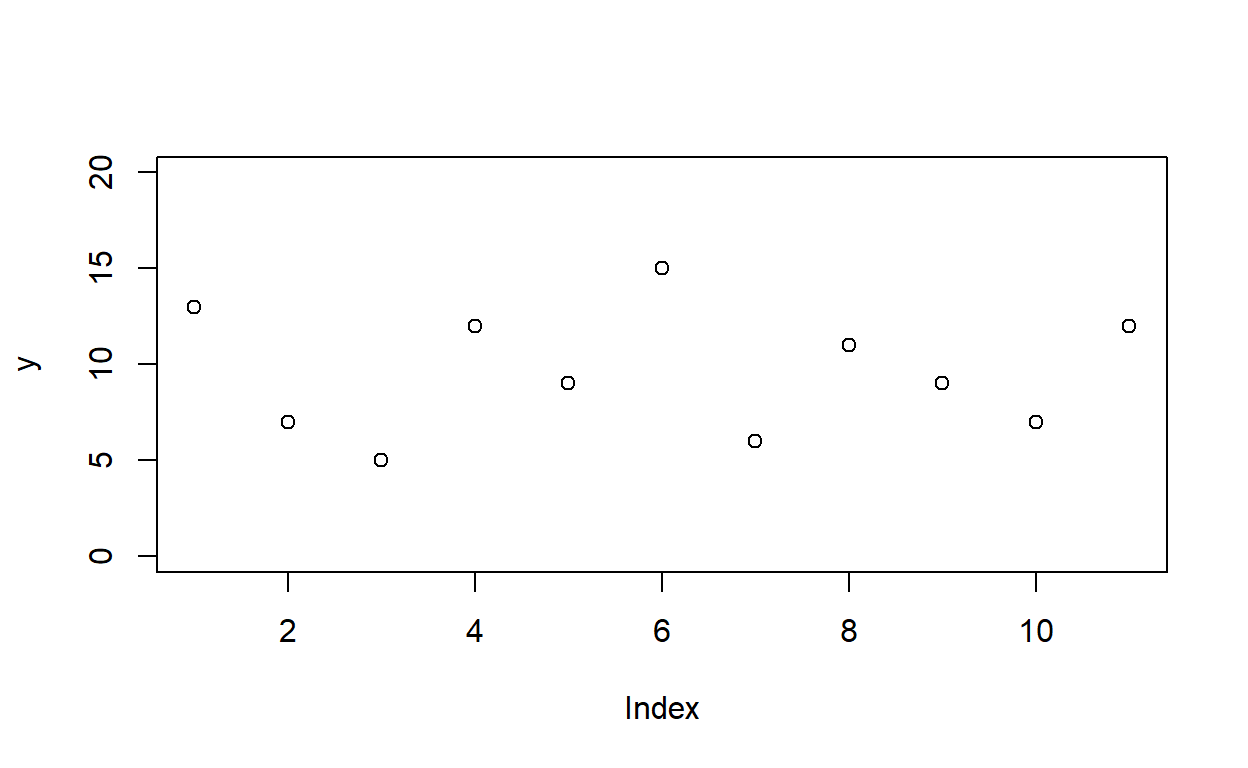
y<-c(13,7,5,12,9,15,6,11,9,7,12)

veamos cómo se ve

#windows()
plot(y,ylim=c(0,20))

Lo más fácil es decir de donde a donde va (el intervalo).

range(y)

[1]  5 15

Pero esto tiene sus problemas.

No tiene relación con el parámetro población de intervalo.
Incrementa con la n.
Además es muy susceptible a valores atípicos
No considera a todos lo valores.

Otra medida de dispersión muy importante es la varianza. Que está fundamentada en las desviaciones (o residuales) de cada valor con la media

y<-c(13,7,5,12,9,15,6,11,9,7,12)
plot(y,ylim=c(0,20))
abline(mean(y),0)
for (i in 1:11) lines(c(i,i),c(y[i],mean(y)))

se usa la suma de cuadrados de la diferencia de cada valor con la media general como base. ¿Cómo lo calculamos?

y-mean(y)

 [1]  3.3636364 -2.6363636 -4.6363636  2.3636364 -0.6363636  5.3636364
 [7] -3.6363636  1.3636364 -0.6363636 -2.6363636  2.3636364

(y-mean(y))^2

 [1] 11.3140496  6.9504132 21.4958678  5.5867769  0.4049587 28.7685950
 [7] 13.2231405  1.8595041  0.4049587  6.9504132  5.5867769

sum((y-mean(y))^2)

[1] 102.5455

Fantásitico, pero que sucede a SC cada vez que yo adiciono una nueva observación. ¿Que tenemos que hacer?

Si divido entre n, se llama la desviación media de los cuadrados.

C.3

R.4

variance <- function (x)   sum((x-mean(x))^2)/(length(x)-1)
variance(y)

[1] 10.25455

Pero claro, ya está definido.

var(y)

[1] 10.25455

La relación entre la varianza de la muestra y el tamaño de muestra (n)

Lo que vamos a hacer es seleccionar aleatoriamente números de una población que tiene una distribución normal (media 10 y var 4). Esto lo vamos a hacer repetidas veces pero nuestra muestra va a ir incrementando su n desde 3 hasta 31. Vamos a sacar 30 muestras de cada tamaño de muestra. Es decir 30 muestras de 3 números, 30 muestras de 5 números etc. A cada muestra le vamos a calcular su varianza y las vamos a graficar.

# windows()
plot(c(0,32),c(0,15),type="n",xlab="Tamaño de muestra",ylab="Varianza")
for (tm in seq(3,31,2)) {
for( i in 1:30){
x<-rnorm(tm,mean=10,sd=2)
points(tm,var(x)) }}

Ahora pueden ver que la varianza poblacional puede estar muy mal estimada con tamaños de muestra pequeños. Y a medida que aumentamos el tamaño de muestra la probabilidad de que la estimación está muy lejos del parámetro disminuye. Esta es una razón más para elegir muy cuidadosamente el tamaño de muestra. En unas clases vamos a hablar de esto en el contexto de pruebas de hipótesis.

C.4

R.5

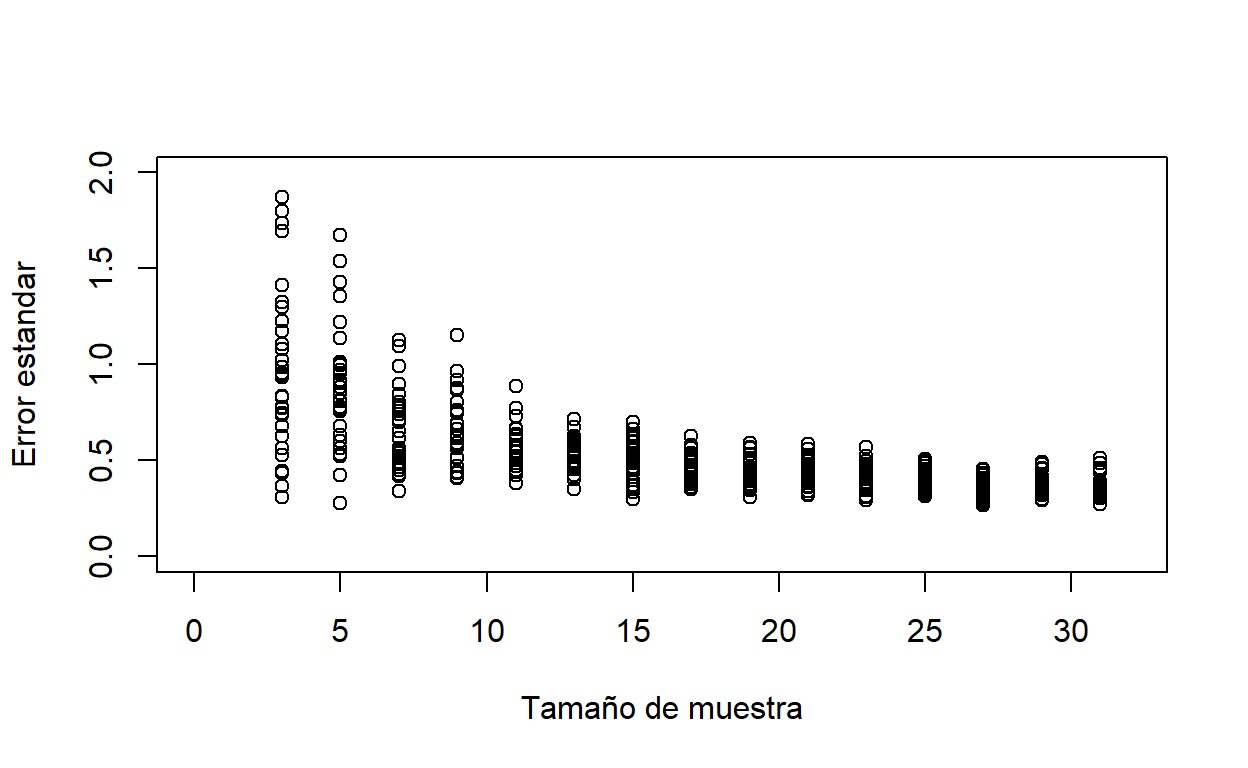
Hagamos el mismo proceso que hicimos antes para elegir muestras con tamaños de muestra que incrementan pero ahora veamos que sucede con nuestra medida de desconfianza de la estimación a medida que aumenta n

#windows()
plot(c(0,32),c(0,2),type="n",xlab="Tamaño de muestra",ylab="Error estandar")
 for (tm in seq(3,31,2)) {
for( i in 1:30){
x<-rnorm(tm,mean=10,sd=2)
points(tm,sqrt(var(x)/tm)) }}

Veamos un ejemplo de la concentración de ozono en unos invernaderos

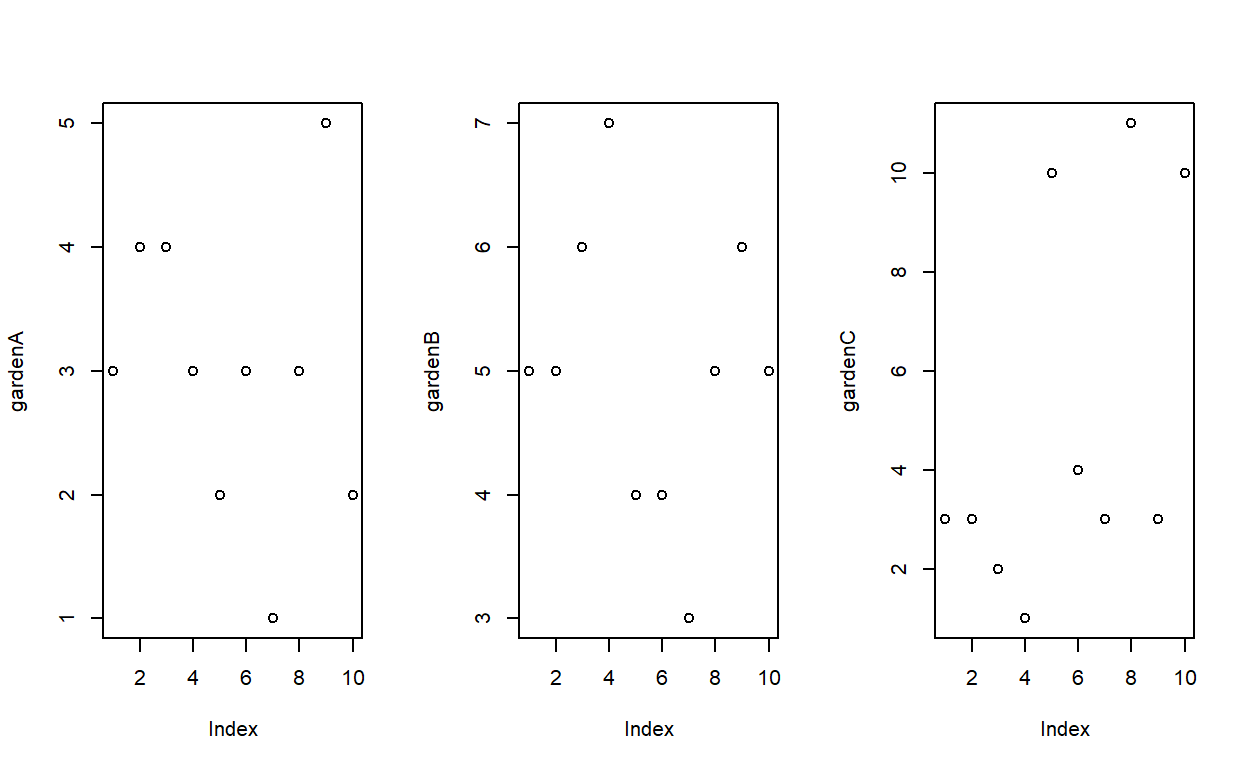
NOTA: Para descargar los datos, dar click en el boton. Aparece una pantalla con los datos, luego dar click derecho y poner guardar como (save as). Guardar el txt donde van a trabajar

ozono<- read.table("gardens.txt",header=T)
attach(ozono)
ozono

#windows()
par(mfrow=c(1,3))
plot (gardenA)
plot (gardenB)
plot (gardenC)

MediaA<- mean(gardenA)
EEA<- sqrt(var(gardenA)/10)
MediaB<- mean(gardenB)
EEB<- sqrt(var(gardenB)/10)
MediaC<- mean(gardenC)
EEC<- sqrt(var(gardenC)/10)

MediaA

[1] 3

EEA

[1] 0.3651484

MediaB

[1] 5

EEB

[1] 0.3651484

MediaC

[1] 5

EEC

[1] 1.19257

¿Para cual invernadero puedo yo confiar más de la estimación de la media?

C.5

R.6

Vamos a calcular los intervalos de confianza para la media de los invernaderos usando la distribución de t. qt nos d? el valor de t para el cual hay cierta proporción a la izquierda.

qt(.975,9)

[1] 2.262157

calculemos los intervalos de confianza al 95% para el invernadero B

qt(.975,9)*sqrt(1.3333/10)

[1] 0.8260127

el reporte diario, la concentración promedio de ozono en el invernadero B fue de 5.0?0.826(I.C.95%, n=10)

#windows()
plot(gardenB)
abline(mean(gardenB),0)
abline((mean(gardenB)+0.826),0, lty=2)
abline((mean(gardenB)-0.826),0, lty=2)

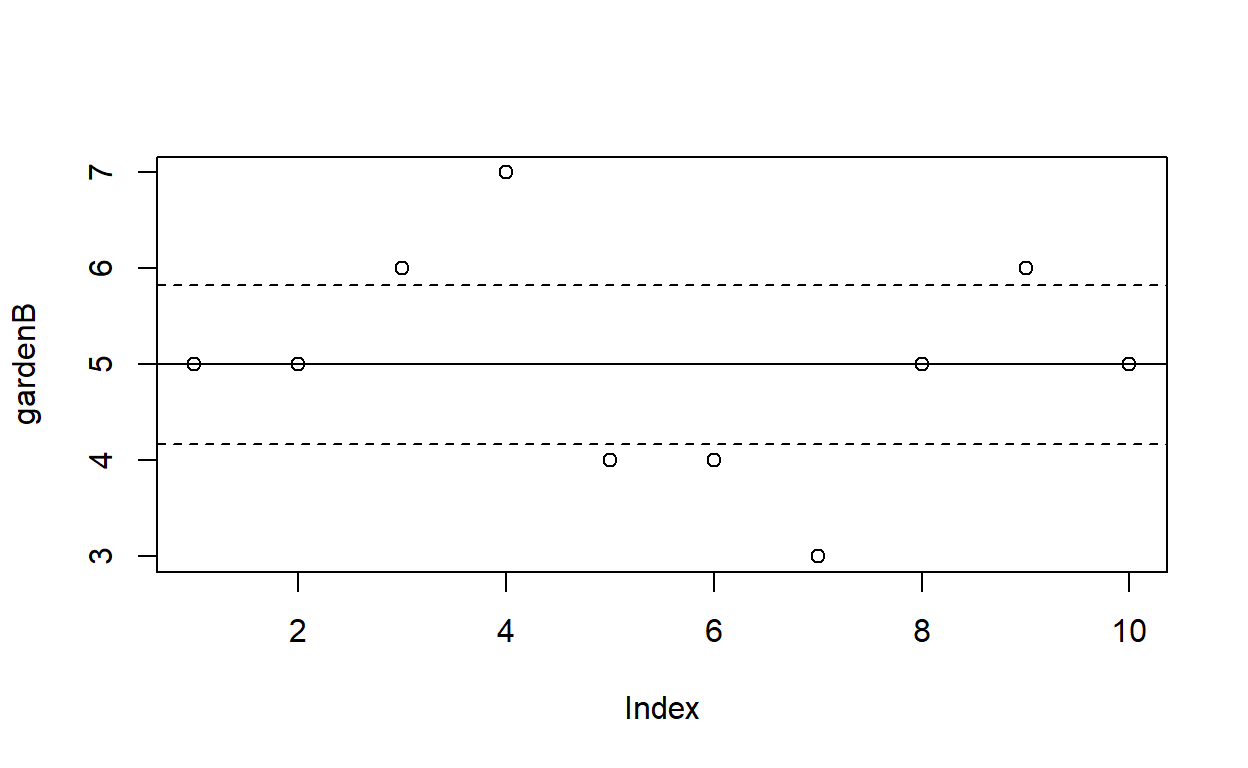
los dejo que ustedes calculen aquellos de los invernaderos A y C.

C.6 Fin ———————————————————————

Script Estimación 2

R.1

Estimación de parámetros de tendencia central

C.1

R.2

C.2

R.3

Medidas de dispersión

C.3

R.4

C.4

R.5

C.5

R.6

C.6

Fin ———————————————————————