Script estimacion 2_bis

NOTA: Para descargar los datos, dar click en el boton. Aparece una pantalla con los datos, luego dar click derecho y poner guardar como (save as). Guardar el txt donde van a trabajar

Intervalos de confianza

Existe otra manera enteramente distinta de estimar intervalos de confianza, y esta es enteramente autoreferida. Se usa el método de remuestreo o bootstrapping. Veamos un cuerpo de datos.

data<-read.table("skewdata.txt",header=T)
attach(data)
names(data)

vamos a verlos visual y gráficamente

values

 [1] 81.372918 25.700971  4.942646 43.020853 81.690589 51.195236
 [7] 55.659909 15.153155 38.745780 12.610385 22.415094 18.355721
[13] 38.081501 48.171135 18.462725 44.642251 25.391082 20.410874
[19] 15.778187 19.351485 20.189991 27.795406 25.268600 20.177459
[25] 15.196887 26.206537 19.190966 35.481161 28.094252 30.305922
hist(values)

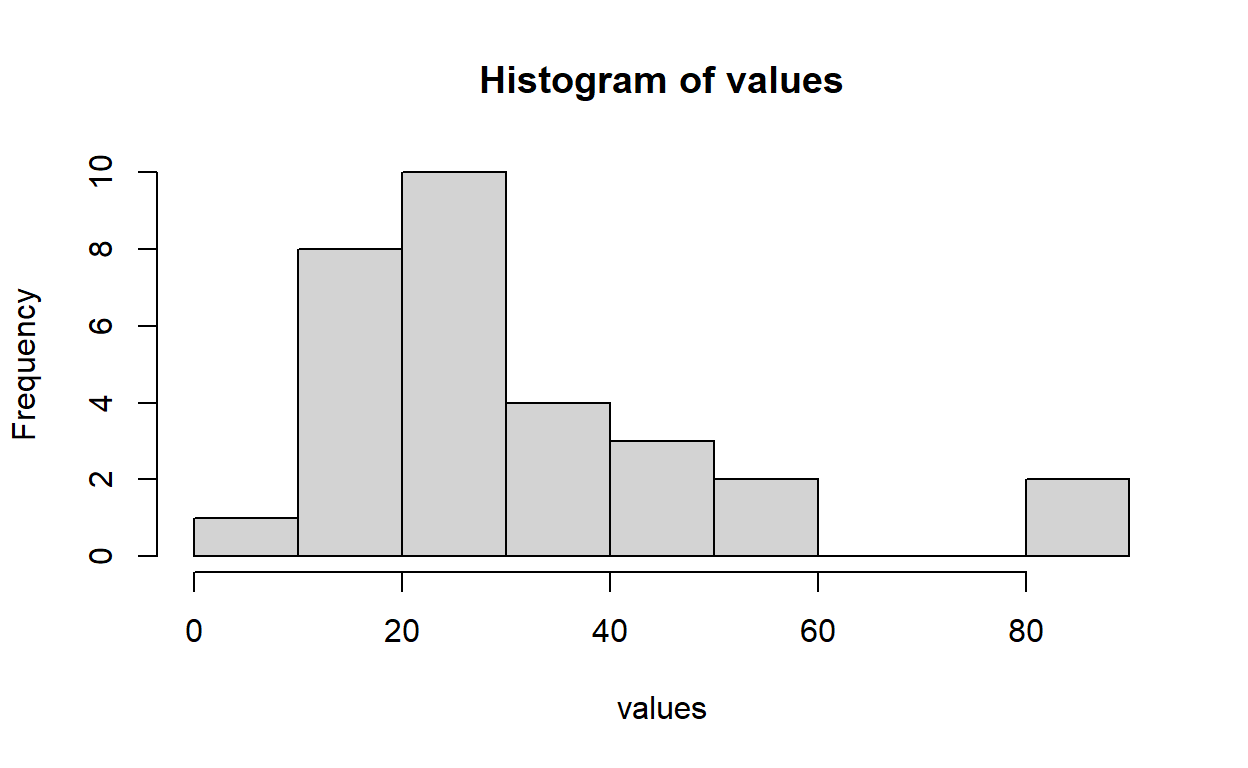
Ahora vamos a calcular los intervalos de confianza de remuestreo por quantiles a través de la función sample que remuestrea y la función quantile basados en la muestra. Ahora, la función construida creo que no existe, así que aquí la definimos.

Remuestreo<-function(x){
a<-numeric(10000)
for (i in 1:10000){
a[i]<-mean(sample(x,30,replace=T))}
quantile(a,c(.025,.975))}
Remuestreo(values)

    2.5%    97.5% 
24.89675 37.86573

Veamos como comparan con los IC normales

mean(values)+1.96*sqrt(var(values)/30)

[1] 37.53846
mean(values)-1.96*sqrt(var(values)/30) 

[1] 24.39885

Vean ustedes porque elegimos 30 como una n buena para tamaño de las muestras repetidas

plot(c(0,60),c(0,60),type="n",xlab="Tamaño de muestra",ylab="IC remuestreo")
 
for (k in seq(5,60,3)){
a<-numeric(10000)
for (i in 1:10000){
a[i]<-mean(sample(values,k,replace=T))
}
points(c(k,k),quantile(a,c(.025,.975)),type="b")
}

# Ahora veamos como comparan con los valores de IC normales
xv<-seq(5,60,0.1)
yv<-mean(values)+1.96*sqrt(var(values)/xv)
lines(xv,yv)
yv<-mean(values)-1.96*sqrt(var(values)/xv)
lines(xv,yv)

#y los valores de IC de t student 

yv<-mean(values)-qt(.975,xv)*sqrt(var(values)/xv)
lines(xv,yv,lty=2)
yv<-mean(values)+qt(.975,xv)*sqrt(var(values)/xv)
lines(xv,yv,lty=2)

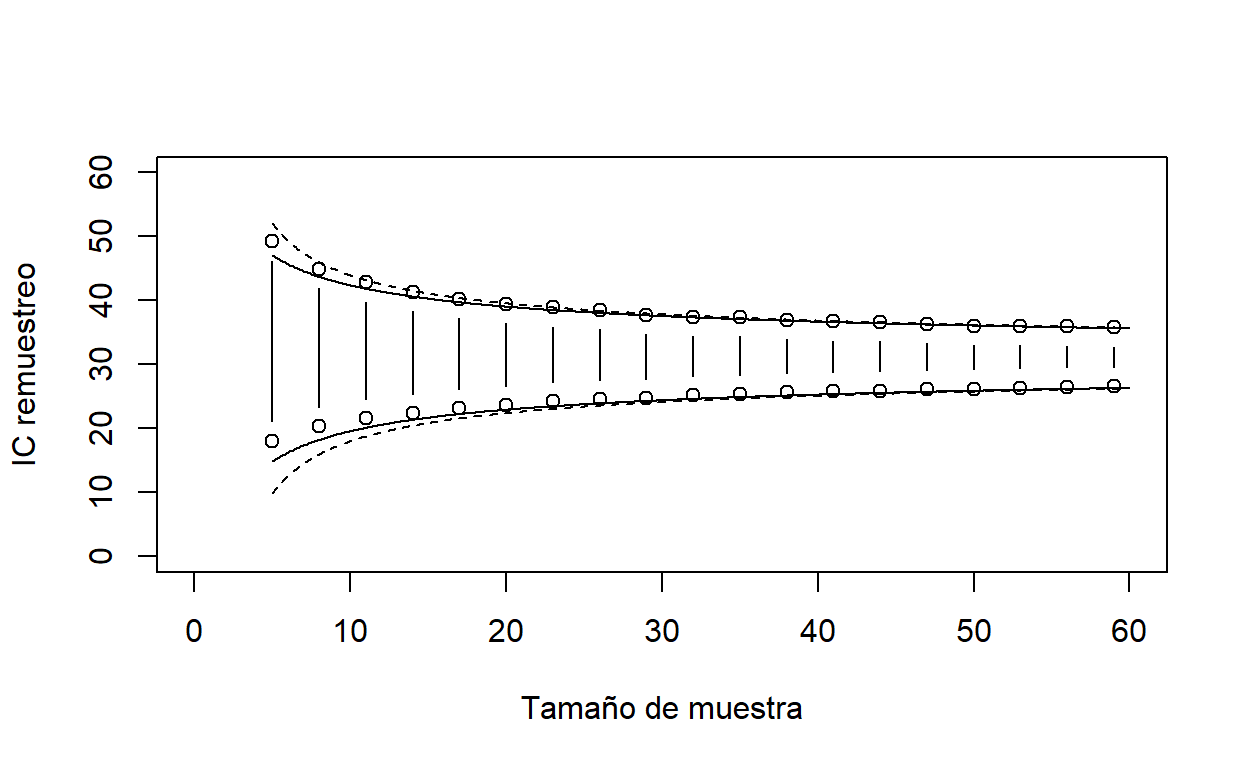
Noten que no son exactamente simétricos. Esto hace que sean ligeramente sesgados. Existen otros dos métodos (por centiles y acelerados) que corrigen esto. También noten que para la distribución de t son más conservadores si el tamaño de muestra es pequeño.

C.6