Script ANDEVA de una via

NOTA: Para descargar los datos, dar click en el boton. Aparece una pantalla con los datos, luego dar click derecho y poner guardar como (save as). Guardar el txt donde van a trabajar

R.1

Conceptos básicos del análisis de la varianza

La hipótesis nula en un análisis de la varianza tipo I común es:

\[H0: m1 = m2 = m3 = ... = mk\]

¿Cómo es que esta hipótesis se pone a prueba en un ANDEVA? Por cierto esta es una prueba “omnibus”, es decir ¡prueba muchas cosas de un jalón!

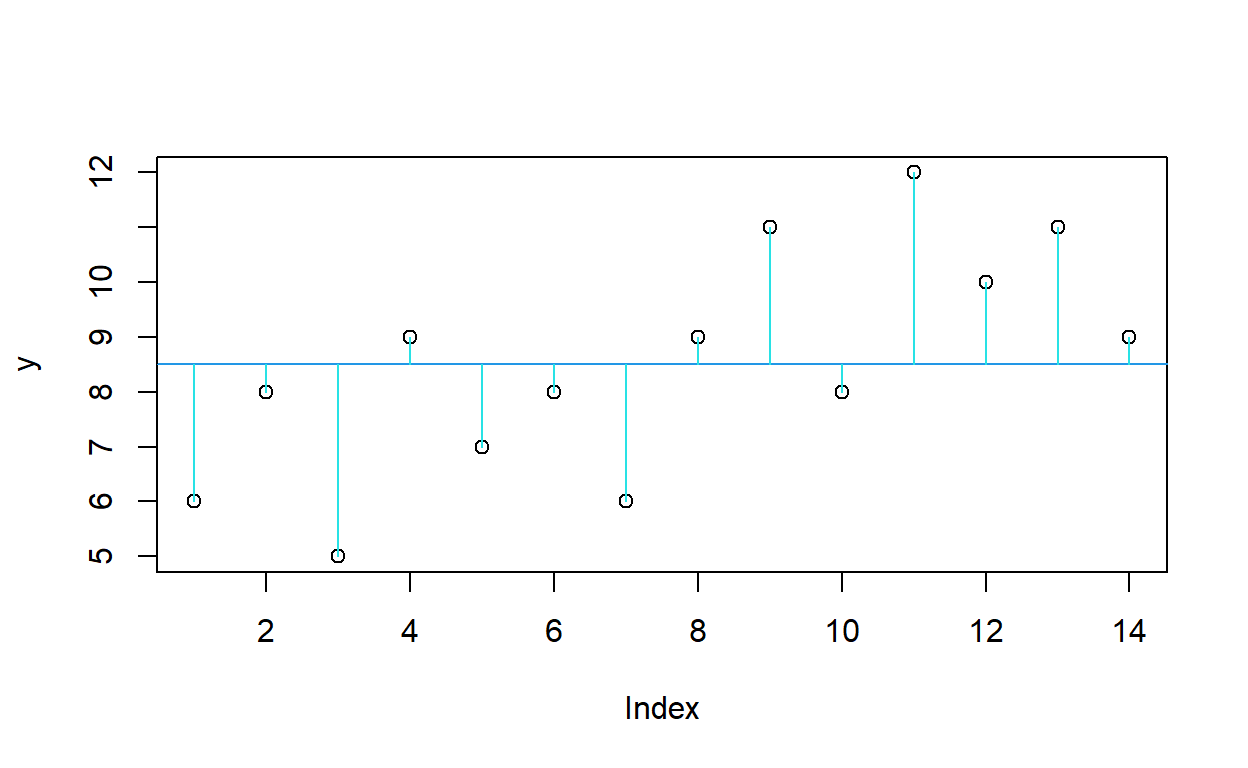
Para ver como es que opera el anova veamos el ejemplo que sigue: Tomemos un solo factor, “f”, con dos niveles y pongamos los datos en una gráfica simple, según el orden en el que fueron obtenidas las mediciones.

anova<-read.table("anova.data.txt",header=T)
attach(anova)
names(anova)

plot(y)
abline(mean(y), 0, col=4)
for (i in 1:length(y)) lines (c(i,i), c(mean(y), y[i]), col=5)

¿Qué muestra esta gráfica? ¿A que equivale la suma de los trazos verticales?

\[ SCT=\Sigma(y- \overline{y})^2\]

Ahora vamos a hacer exactamente lo mismo, pero ahora dividiendo por cada uno de los niveles del factor F. Incorporemos la información del factor “f”. Para esto hay que calcular los promedios de “y” que corresponden a los niveles de “f”

promedios <- tapply(y, f, mean)

Grafiquemos esta nueva estructura de datos sobre la gráfica que ya tenemos

plot(y)
lines(c(1, 7), c(promedios[1], promedios[1]), col = 2)
lines(c(7, 14), c(promedios[2], promedios[2]), col = 5)
for (i in 1:7 ) lines (c(i,i), c(promedios[1], y[i]), col = 1, lty=6)
for (i in 8:14) lines (c(i,i), c(promedios[2], y[i]), col = 1, lty=6)

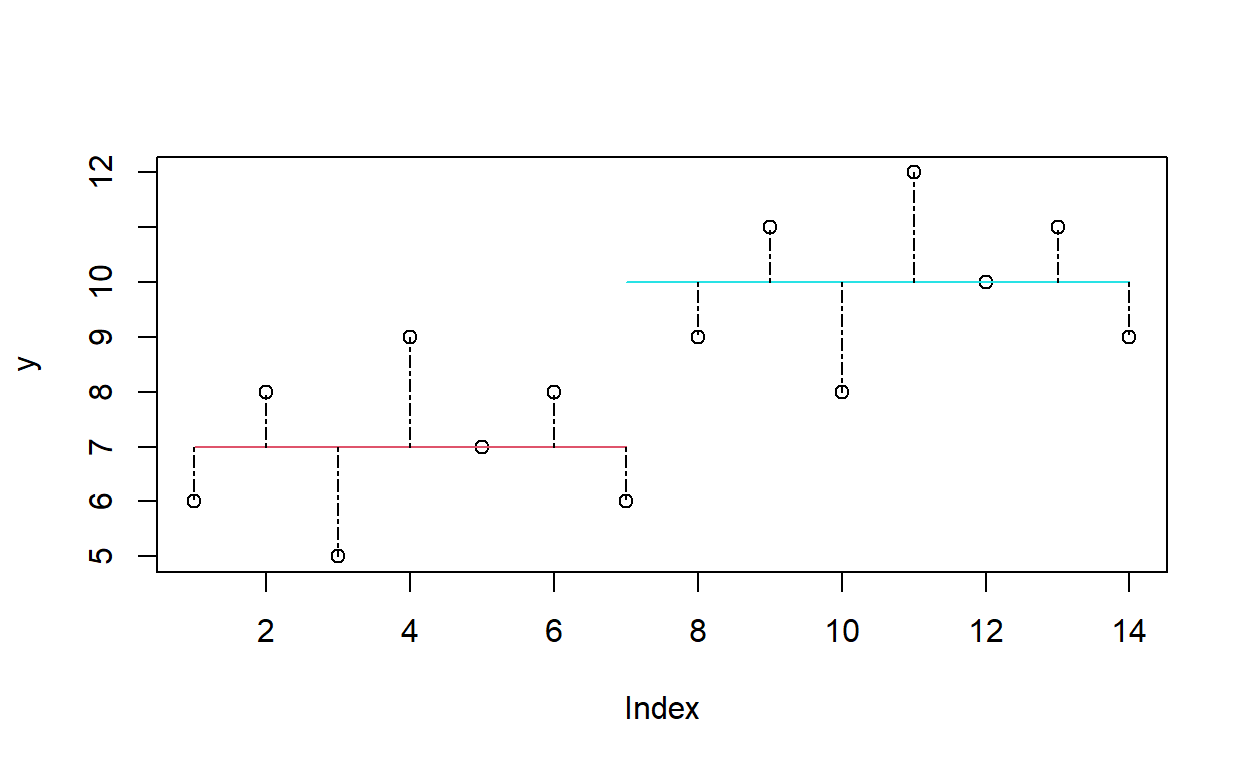
¿Qué muestra esta gráfica? ¿a que equivale la suma de los trazos punteados verticales?

\[SCE= \Sigma(y_1-\hat{y_1})^2 + \Sigma(y_2- \hat{y_2})^2\]

Si las dos medias fueran iguales ¿cómo compararían estas dos gráficas?

Si lo piensan tendrían que ser iguales porque las medias de los niveles del tratamiento se nivelarían a la misma altura. Si las medias son significativamente distintas ¿cual varianza sería mayor? la calculada con SCT o la calculada con SCE? Esta es la razón por la cual el ANDEVA compara medias a través de la comparación de varianzas!!!!

¿Qué interpretación tiene la diferencia entre las dos sumas mencionadas arriba? Pues es precisamente la varianza explicada por el modelo. Esta diferencia se asocia con la siguiente gráfica:

modelo <- lm(y~f)
plot (y)
abline (mean(y), 0, col = 4)
points(predict(modelo), pch = 16, col = 5)
for (i in 1:14) lines(c(i, i), c(mean(y), predict(modelo)[i]), col = 6)

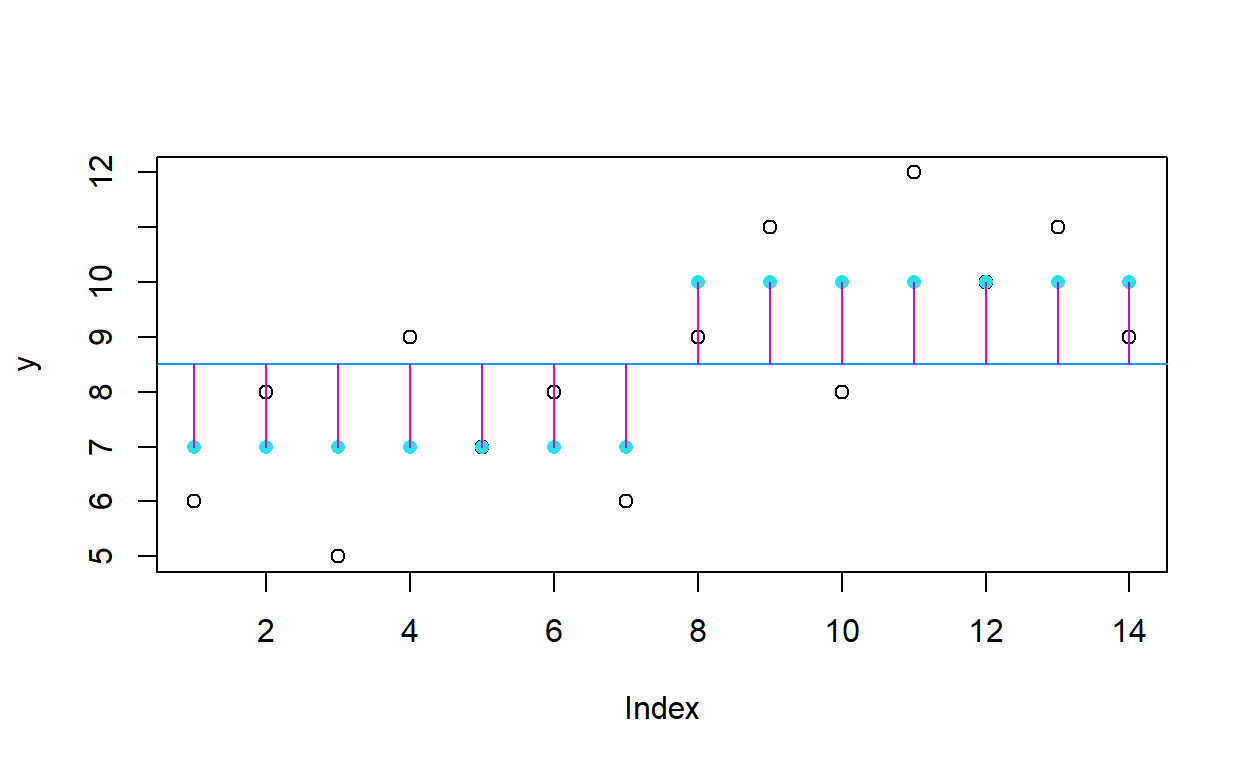
C.1

R.2

¿Que implica el ajuste del modelo ANOVA del factor “f”?

SCT<-sum((y-mean(y))^2)
SCT

[1] 55.5

La pregunta es cuanto de esta variación es explicada por diferencias entre las medias de A y B (niveles del factor F) y cuanto por el error

SCEa<-sum((y[f=="a"]-mean(y[f=="a"]))^2)
SCEb<-sum((y[f=="b"]-mean(y[f=="b"]))^2)

Entonces la SCE es la suma de estas dos cantidades

SCE<-SCEa+SCEb
SCE

[1] 24

Finalmente la SCA es SCT-SCE

SCA<-SCT-SCE
SCA

[1] 31.5

Entonces ya podemos llenar la tabla de ANOVA

#C.2

R.3

Ahora calculemos la F

31.5/2

[1] 15.75

y la p

1-pf(15.75,1,12)

[1] 0.001864103

Ahora el automatico

modelo<-aov(y~f)

summary(modelo)

            Df Sum Sq Mean Sq F value  Pr(>F)   
f            1   31.5    31.5   15.75 0.00186 **
Residuals   12   24.0     2.0                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
boxplot(y~f,xlab="factor F",ylab="y")

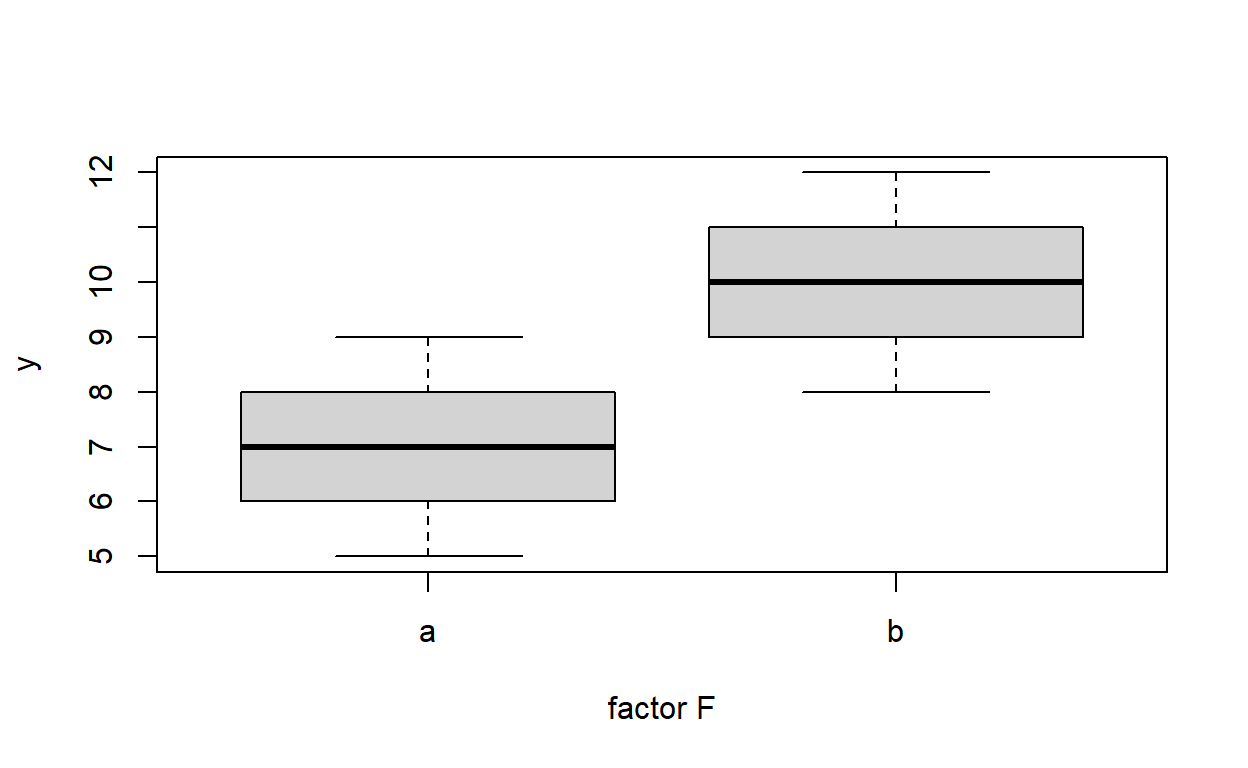
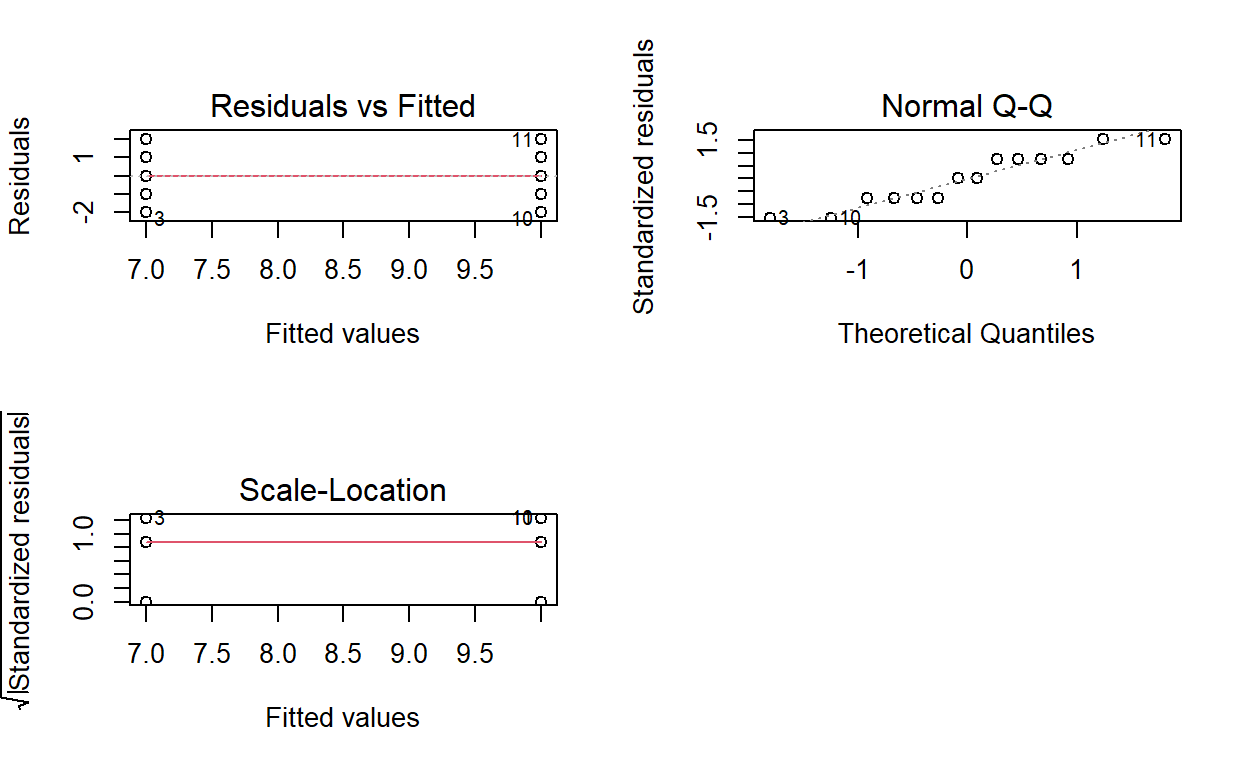
¿Cual es la conclusión? Ahora hacemos la crítica del modelo

par(mfrow=c(2,2))
plot(modelo)

y ahora lo ultimo

A<-c(6,8,5,9,7,8,6)
B<-c(9,11,8,12,10,11,9)
t.test(A,B)


    Welch Two Sample t-test

data:  A and B
t = -3.9686, df = 12, p-value = 0.001864
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -4.647028 -1.352972
sample estimates:
mean of x mean of y 
        7        10 
summary(modelo)

            Df Sum Sq Mean Sq F value  Pr(>F)   
f            1   31.5    31.5   15.75 0.00186 **
Residuals   12   24.0     2.0                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

La anova es una “Generalización” de t para poder comparar mas de dos medias. En realidad F=t^2

Fin