Script `DivOC_script.R`

1. Instalar y cargar el paquete —-

Comenzaremos usando la paquetería DiversityOccupancy. Este paquete estima la diversidad alfa por medio de modelos jerárquicos.

# install.packages("DiversityOccupancy")

library(DiversityOccupancy)
library(camtrapR) #Funciones de registro de especies
library(tidyverse) # Manípular datos y gráficos
library(hillR) # Estimar diversidad
library(ggeffects) #gráficas de pred para glm
library(beepr) # Opcional para avisar R termine
library(tictoc) # Opcional para tomar el tiempo de la función

Este paquete te va a pedir instalar también MuMIn, unmarked, reshape, lattice, Rcpp

2. Cargar los datos —-

Formato de los datos

Son necesarios eventos de muestreo repetidos. Vamos a trabajar con una base de datos de 17 especies, 67 sitios (cámaras) y 19 eventos de muestreo.

Nota: Todas las especies deben tener una matriz de historias de detección de las mismas dimensiones

# Cargamos la tabla de registros de las especies
registers <-  read.csv("Data/Survey/recordTable_OC.csv")
table(registers$Species)


     Bassariscus astutus            Canis latrans 
                       3                        6 
  Canis lupus familiaris             Capra hircus 
                       4                       13 
    Conepatus leuconotus     Dasypus novemcinctus 
                      79                        1 
              Lynx rufus        Mephitis macroura 
                      50                       18 
            Nasua narica   Odocoileus virginianus 
                       4                      227 
           Pecari tajacu            Procyon lotor 
                      71                       40 
       Puma yagouaroundi                 Roedores 
                       6                       66 
  Spilogale angustigrons    Sylvilagus floridanus 
                      13                      492 
Urocyon cinereoargenteus 
                     173

# Cargamos la tabla de operación de cámaras
CToperation <-  read.csv("Data/Survey/CTtable_OC.csv") 

# Generamos la matríz de operación de las cámaras

camop <- camtrapR::cameraOperation(CTtable= CToperation, # Tabla de operación
                         stationCol= "Station", # Columna que define la estación
                         setupCol= "Setup_date", #Columna fecha de colocación
                         retrievalCol= "Retrieval_date", #Columna fecha de retiro
                         hasProblems= T, # Hubo fallos de cámaras
                         dateFormat= "%Y-%m-%d") # Formato de las fechas

# Función para generar las historias de detección para todas las especies seleccionadas

DetHist_list <- lapply(unique(registers$Species), FUN = function(x) {
  detectionHistory(
    recordTable         = registers, # Tabla de registros
    camOp                = camop, # Matriz de operación de cámaras
    stationCol           = "Station",
    speciesCol           = "Species",
    recordDateTimeCol    = "DateTimeOriginal",
    recordDateTimeFormat  = "%d/%m/%Y",
    species              = x,     # la función reemplaza x por cada una de las especies
    occasionLength       = 10,  # Colapso de las historias a 10 días
    day1                 = "station", #inicie en la fecha de cada estación
    datesAsOccasionNames = FALSE,
    includeEffort        = TRUE,
    scaleEffort          = TRUE,
    timeZone             = "America/Mexico_City" 
  )}
)

# Se genera una lista con cada historia de detección y el esfuerzo de muestreo, ahora le colocaremos los nombres para saber a cual especie corresponde
names(DetHist_list) <- unique(registers$Species)

# Finalmente creamos una lista nueva donde estén solo las historias de detección
ylist <- lapply(DetHist_list, FUN = function(x) x$detection_history)

# Todas las historias deben tener el mismo número de sitios y de ocasiones de muestreo

data <- ylist %>% # Lista con los datos
  reduce(cbind) # Unimos las historias de captura en un solo dataframe

Obtenemos una matriz con el mismo número de sitios 67 y 19 eventos X 17 especies = 323 columnas

	o1	o2	o3	o4	o6	o7	o8	o9	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o5	o6	o7	o9	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o4	o5	o6	o7	o8	o9	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o4	o5	o6	o7	o8	o9	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o9	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o7	o9	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o4	o5	o6	o7	o8	o9	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o7	o8	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o7	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o4	o6	o7	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o11	o12	o13	o14	o15	o16	o17	o18	o19	o1	o2	o3	o11	o12	o13	o14	o15	o16	o17	o18	o19
C1T2P1	0	0	0	0	0	1	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	1	1	1	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	1	1	1	1	1	1	1	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	0	0	0	0	0	1	0	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA
C1T2P11	NA	NA	NA	1	1	0	1	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	0	1	1	1	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	1	1	0	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	1	0	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
C1T2P21	0	0	0	0	0	0	0	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	1	1	1	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	1	1	0	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	1	1	0	1	0	0	1	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	1	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA
C1T4P1	0	0	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	1	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA
C1T4P11	1	0	1	0	0	1	1	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	1	1	1	1	1	1	1	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	1	1	1	1	0	1	1	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	1	1	1	0	1	0	1	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	0	1	1	1	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA
C1T4P21	0	0	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	NA

Cargar las covariables

Vamos a leer el archivo .csv de la ruta data/Covs/ que contiene las covariables de sitio (no usaremos de observación). Todas estas estandarizadas

# Ahora cargamos las covariables (previamente estandarizadas)
covars <- read.csv("Data/Covs/stdcovs_OC.csv") %>% 
  select(-"...1", -X, -Station, -Cam, -Cluster) # Las gráficas no funcionan con categóricas

Vertcover_50	Dcrops	MSAVI	Slope	Effort	Dpop_G
-0.4744602	0.6765368	0.7316819	-0.2195550	-0.2080680	-0.4260974
0.6519157	1.4620448	-0.8666152	-0.9927301	-1.4605398	-0.3167450
-0.9243340	2.2193059	-0.5838870	-1.0258694	-0.0719298	-0.1805434
-0.9243340	0.4603495	-0.1430110	1.4183658	-0.8887592	-0.1922714

Importante: Cada proceso es afectado por diferentes covariables. Para más información mira este enlace

3. Modelos de abundancia —-

3.1 Modelos básicos —-

Vamos a utilizar la función diversityoccu(). Se genera un objeto lista con los modelos para cada una de las especies, cálculo de diversidad y otras cosas….

cam_diver <- diversityoccu(pres = data, # La matriz de datos
     sitecov = covars, # Covariables de sitio
     obscov = NULL, # no tenemos covariables de observación,
     spp = 17, # Número de especies
     form = ~ Effort + Slope ~ Dcrops, # Formula del modelo p(), lambda()
     dredge = FALSE # En este primer ejemplo no usaremos AIC
     )

[1] "Species 1 ready!"
[1] "Species 2 ready!"
[1] "Species 3 ready!"
[1] "Species 4 ready!"
[1] "Species 5 ready!"
[1] "Species 6 ready!"
[1] "Species 7 ready!"
[1] "Species 8 ready!"
[1] "Species 9 ready!"
[1] "Species 10 ready!"
[1] "Species 11 ready!"
[1] "Species 12 ready!"
[1] "Species 13 ready!"
[1] "Species 14 ready!"
[1] "Species 15 ready!"
[1] "Species 16 ready!"
[1] "Species 17 ready!"

Se va a generar un objeto lista con los modelos para cada una de las especies, cálculo de diversidad y otras cosas….

Veamos uno de los modelos 🐺

cam_diver$models[[9]] # Modelo para la especie 9


Call:
occuRN(formula = form, data = data2)

Abundance:
            Estimate    SE      z P(>|z|)
(Intercept)  -0.1543 0.278 -0.555   0.579
Dcrops       -0.0306 0.190 -0.161   0.872

Detection:
            Estimate    SE     z  P(>|z|)
(Intercept)   -2.835 0.339 -8.37 5.54e-17
Effort         0.909 0.324  2.81 4.99e-03
Slope         -0.596 0.216 -2.76 5.78e-03

AIC: 317.6726

No sabemos si todas las especies responden de la misma manera a las covariables que usamos. Debemos escoger de todas las variables cual se ajusta mejor a cada especie

¿Cómo vamos a generar todas las posibles combinaciones de modelos para cada especie?

3.2 Mejores modelos con AIC —-

Tranquilo esta misma función lo hace por ti :D. Solamente tenemos que activar dredge

Dependiendo de tu computador la función puede tardar más o menos. En la mía duró ~57 segs. Pero puede tardar mucho más dependiendo del número de especies, sitios, eventos de muestreo y cantidad de covariables.

cam_diver_AIC <- diversityoccu(pres = data, # La matriz de datos
                           sitecov = covars, # Covariables de sitio
                           obscov = NULL, # no tenemos covariables de observación,
                           spp = 17, # Número de especies
                           form = ~ Effort + Slope ~ Dcrops, # Formula del modelo p(), lambda()
                           dredge = TRUE # escoge los mejores modelos con AIC
)

Veamos de nuevo el modelo que seleccionó para la sp9 🐺

cam_diver$models[[9]]


Call:
occuRN(formula = form, data = data2)

Abundance:
            Estimate    SE      z P(>|z|)
(Intercept)  -0.1543 0.278 -0.555   0.579
Dcrops       -0.0306 0.190 -0.161   0.872

Detection:
            Estimate    SE     z  P(>|z|)
(Intercept)   -2.835 0.339 -8.37 5.54e-17
Effort         0.909 0.324  2.81 4.99e-03
Slope         -0.596 0.216 -2.76 5.78e-03

AIC: 317.6726

cam_diver_AIC$models[[9]]


Call:
occuRN(formula = ~Effort + Slope + 1 ~ 1, data = data2)

Abundance:
 Estimate    SE      z P(>|z|)
   -0.145 0.272 -0.532   0.595

Detection:
            Estimate    SE     z  P(>|z|)
(Intercept)   -2.846 0.333 -8.54 1.30e-17
Effort         0.925 0.308  3.01 2.62e-03
Slope         -0.596 0.215 -2.77 5.58e-03

AIC: 315.6987

3.3 Gráfico de predicción —-

Veamos el resultado gráfico para la especie 3

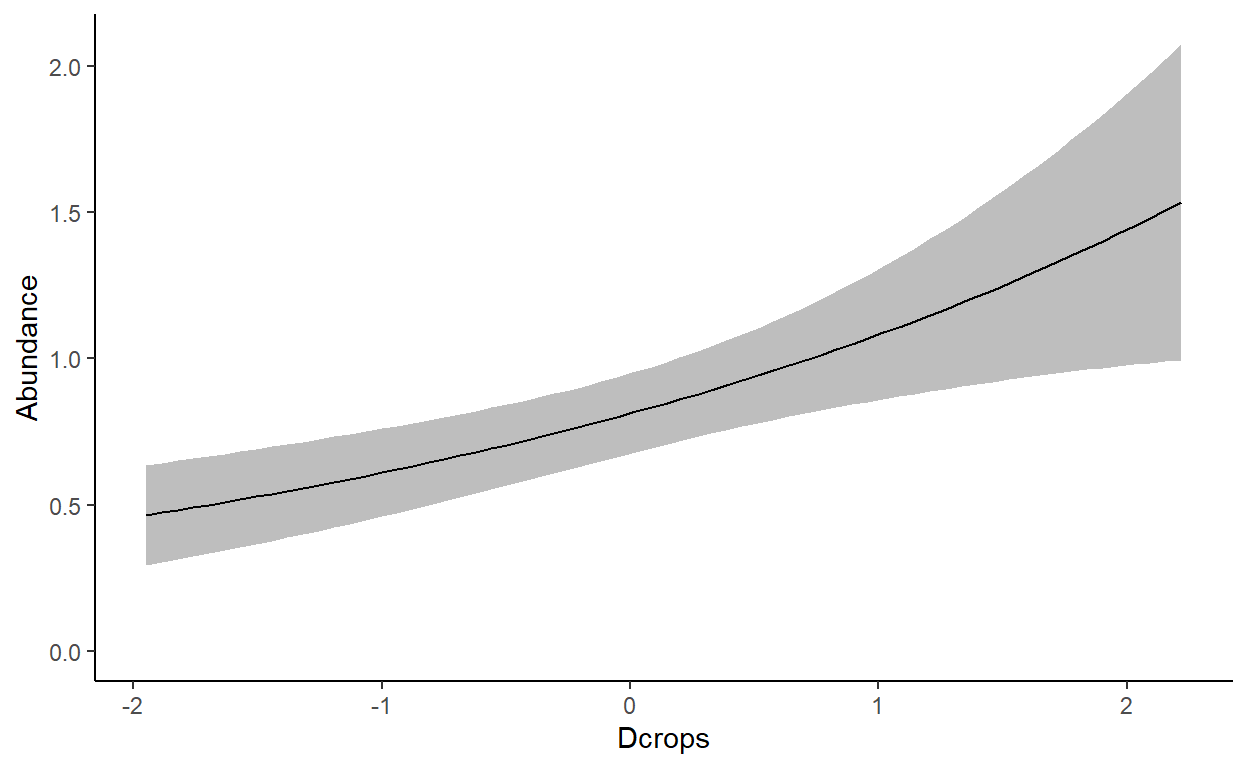
(responseplot.abund( batch = cam_diver_AIC, # objeto creado con diversityoccu
                    spp = 3, # número o nombre de la sp
                    variable= Dcrops # variable  
))

4. Modelando la diversidad —-

Tenemos un modelo donde se estima la abundancia para cada especie, es hora de modelar la diversidad

glm.div <- model.diversity(DivOcc = cam_diver_AIC,# modelos
                           method = "h", # método
                           delta = 2, 
                           squared = T # términos cuadráticos
                                                     )

AICtab <- glm.div$Table

model	aicc	weights	Delta.AICc
Diversity ~ 1 + Dcrops + I(Dcrops^2)	-331.8899	0.3229081	0.0000000
Diversity ~ 1 + Vertcover_50 + Dcrops + I(Dcrops^2)	-331.3285	0.2438852	0.5613404
Diversity ~ 1 + Dcrops + MSAVI + I(Dcrops^2)	-330.5617	0.1662141	1.3281821
Diversity ~ 1 + Dcrops + MSAVI + I(Dcrops^2) + I(MSAVI^2)	-330.3166	0.1470432	1.5732824
Diversity ~ 1 + Dcrops + Dpop_G + I(Dcrops^2)	-329.9093	0.1199495	1.9805941

4.1 Respuesta Gráfica de la diversidad a distintas variables —-

Ahora veamos la respuesta gráfica de la diversidad a una variable

responseplot.diver(glm.div, Dcrops)

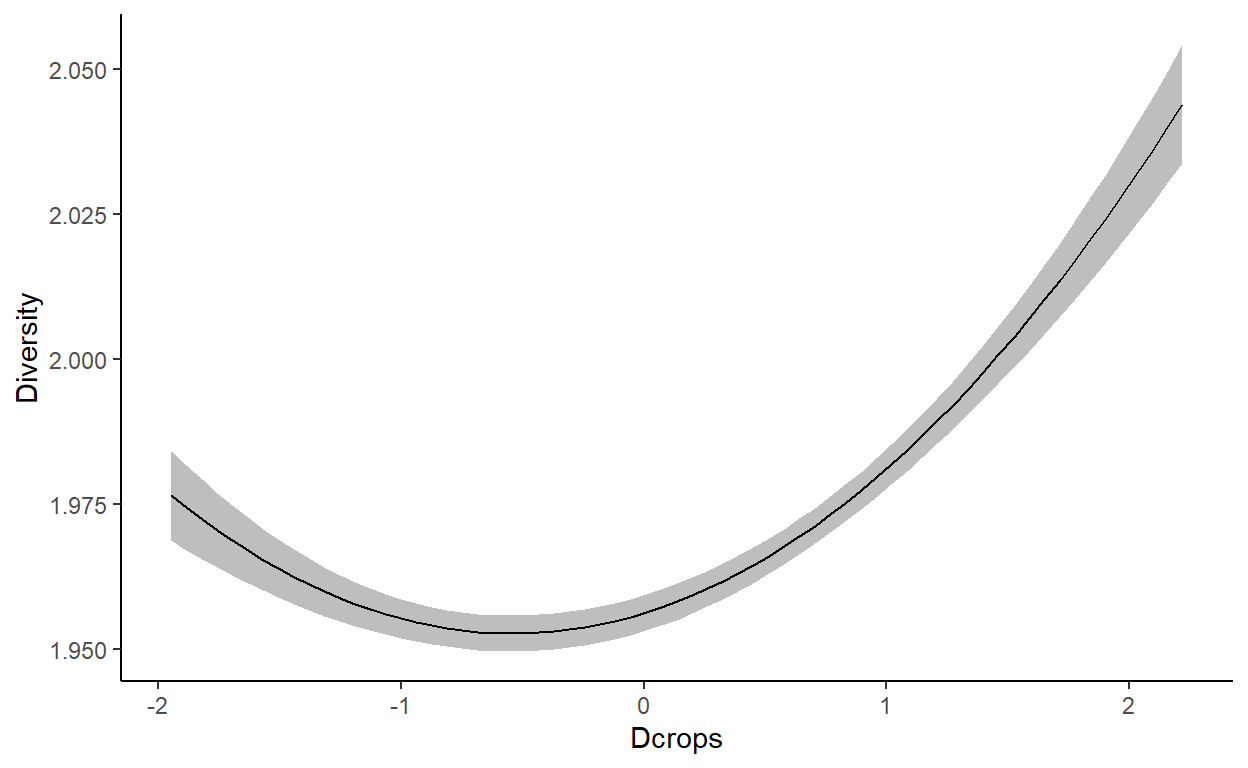
A medida que aumenta el valor de distancia a cultivos (escalado) hay mayor diversidad ?????

Relativamente fácil, para ser verdad …..

Si seguimos la viñeta del paquete nunca nos dice que elemento de la diversidad mide o calcula..

Riqueza?
Shannon, simpson?….
Número efectivo de especies?? (Hill)

Glm? de que tipo?

Un Glm puede ser de varias familias (distribuciones) y depende de la naturaleza de los datos: conteos, proporciones, unos y ceros

Es importante leer el manual

4.2 Diversidad para cada indice de entropía

Hay otro argumento de la función diversityoccu y es “index”. Este argumento permite escoger que índice utilizar “shannon”, “simpson” o “invsimpson”.

cam_diver_sh <- diversityoccu(pres = data, 
                           sitecov = covars, 
                           obscov = NULL, 
                           spp = 17, 
                           form = ~ Effort + Slope ~ Dcrops,
                           dredge = TRUE, 
                           index = "shannon" #<<
)

Podemos aplicar la función para cada índice…?

También se puede hacer una función que lo haga en automático, pero por simplicidad (~~no se hacerlo bien~~) corremos tres veces la función

cam_diver_sim <- diversityoccu(pres = data, 
                           sitecov = covars, 
                           obscov = NULL, 
                           spp = 17, 
                           form = ~ Effort + Slope ~ Dcrops,                            dredge = TRUE,  
                           index = "simpson" #<<
)

cam_diver_inv <- diversityoccu(pres = data, 
                           sitecov = covars, 
                           obscov = NULL, 
                           spp = 17, 
                           form = ~ Effort + Slope ~ Dcrops,                            dredge = TRUE,  
                           index = "invsimpson" #<<
)

Índices de entropía …..

El problema de estos índices (~~para los ecólogos~~) es que - son adimensionales - no siguen una relación lineal con la riqueza (doble de riqueza \(\neq\) doble de diversidad)

5. Calculamos número efectivo de especies —-

Calculemos el número efectivo de especies con las abundancias estimadas

# Extraer los datos de abundancia
hill_data <- cam_diver_inv[[4]] %>% 
  select(-h)

Sospechoso…

species.1	species.2	species.3	species.4	species.5	species.6	species.7	species.8	species.9	species.10	species.11	species.12	species.13	species.14	species.15	species.16	species.17
0.6082829	1.179013	0.9865411	0.7986634	0.6344764	0.470707	1.73449	2.942110	0.8654214	0.1201388	8.197757	0.1485776	8.906907	0.0098931	0.119418	11.42479	0.237951
0.6082829	1.179013	1.2351996	0.7986634	0.6344764	0.470707	1.73449	6.441039	0.8654214	0.1201388	8.197757	0.1485776	8.906907	0.0014365	0.119418	11.42479	0.237951
0.6082829	1.179013	1.5340820	0.7986634	0.6344764	0.470707	1.73449	13.709316	0.8654214	0.1201388	8.197757	0.1485776	8.906907	0.0002236	0.119418	11.42479	0.237951
0.6082829	1.179013	0.9273586	0.7986634	0.6344764	0.470707	1.73449	2.371387	0.8654214	0.1201388	8.197757	0.1485776	8.906907	0.0168258	0.119418	11.42479	0.237951
0.6082829	1.179013	1.1369200	0.7986634	0.6344764	0.470707	1.73449	4.824359	0.8654214	0.1201388	8.197757	0.1485776	8.906907	0.0029269	0.119418	11.42479	0.237951
0.6082829	1.179013	1.4022314	0.7986634	0.6344764	0.470707	1.73449	10.022276	0.8654214	0.1201388	8.197757	0.1485776	8.906907	0.0004836	0.119418	11.42479	0.237951

Calculemos diversidad con hillR

# calcular los perfiles de diversidad
q0 <- hill_taxa(hill_data, q=0) 
q1 <- hill_taxa(hill_data, q=1)
q2 <- hill_taxa(hill_data, q=2)

Ahora unimos las bases de datos y las covariables para modelar

# Unir las bases de perfiles de diversidad
hill_div <- data.frame(q0=q0, q1=q1, q2=q2)
# Unir con las covariables
glm_hill <- cbind(hill_div, covars)

Obtenemos esta base

q0	q1	q2	Vertcover_50	Dcrops	MSAVI	Slope	Effort	Dpop_G
17	7.290641	5.283733	-0.4744602	0.6765368	0.7316819	-0.2195550	-0.2080680	-0.4260974
17	7.476420	5.687832	0.6519157	1.4620448	-0.8666152	-0.9927301	-1.4605398	-0.3167450
17	7.068294	5.418051	-0.9243340	2.2193059	-0.5838870	-1.0258694	-0.0719298	-0.1805434
17	7.204272	5.173335	-0.9243340	0.4603495	-0.1430110	1.4183658	-0.8887592	-0.1922714
17	7.448817	5.558398	-1.1509622	1.1723154	0.2129457	-0.0597006	-0.0719298	-0.0948151
17	7.342298	5.686248	0.6519157	1.9052628	0.5284530	-1.0258694	-0.0719298	0.0268169

Ahora ajustemos un glm sencillo

glm_q1 <- glm(q1~ Dcrops, family = gaussian, data = glm_hill)

y usemos ggeffects para graficar

plot_q1 <- ggpredict(glm_q1, terms = "Dpop_G")
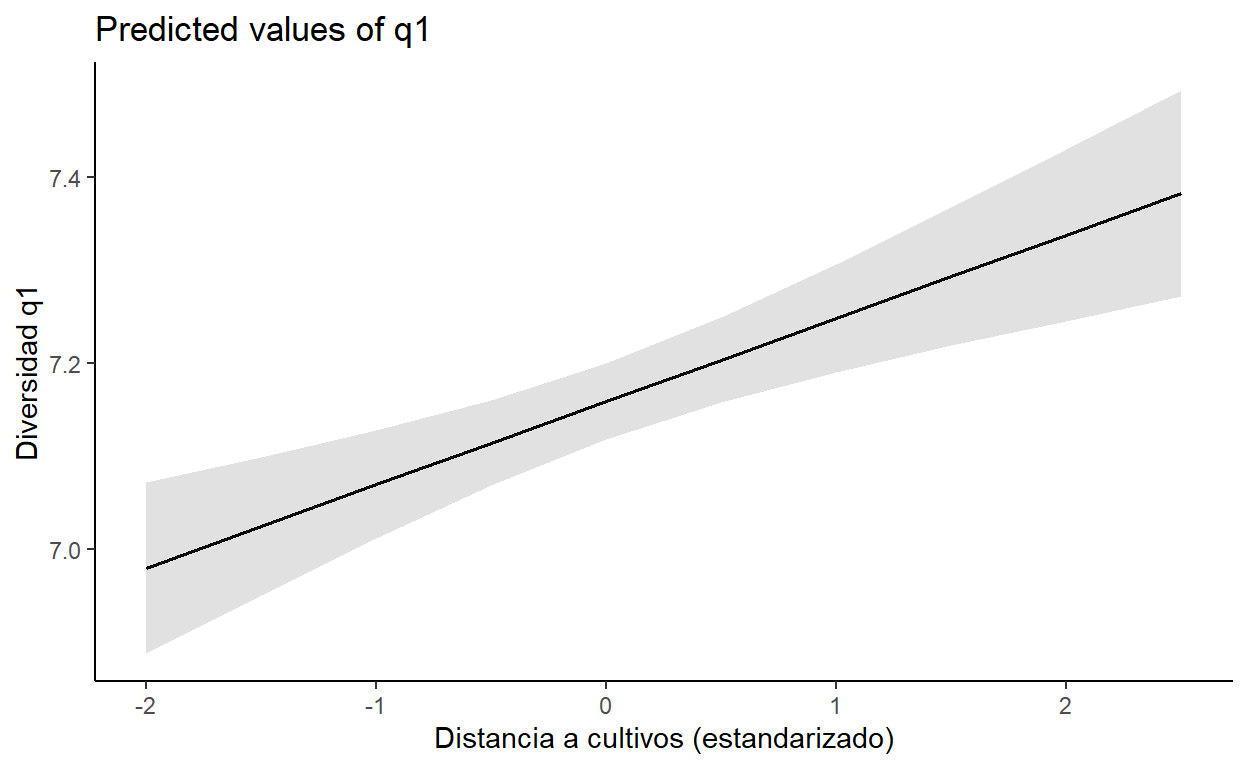
plot(plot_q1)+
  labs(y= "Diversidad q1", 
       x= "Distancia a poblados (estandarizado)")+
  theme_classic()

Tarea

Modelar los otros perfiles de diversidad
Crear modelos candidatos con otras covariables y escoger con AIC

6. Consideraciones finales

El paquete es bueno y agiliza muchos pasos del modelado
Cuando no hay ninguna covariable que explique la “abundancia”, se asume que es constante para todos los sitios. Eso puede subestimar o sobrestimar la abundancia…
“Abundancia” constante: diversidad de la localidad y no de la cámara?
Si se usan los índices de entropía se debe saber cómo interpretarlos (Jost 2006 ; Jost et al 2010)]

7. Ejemplo en una investigación

Un ejemplo de cómo se pueden usar los modelos Royle-Nichols para calcular diversidad

Tesis de licenciatura pregrado premiada por la Asosiación Mexicana de Mastozoología A.C. (AMMAC)

https://www.youtube.com/watch?v=qaD9NRAg3SQ ]

Script DivOC_script.R